|
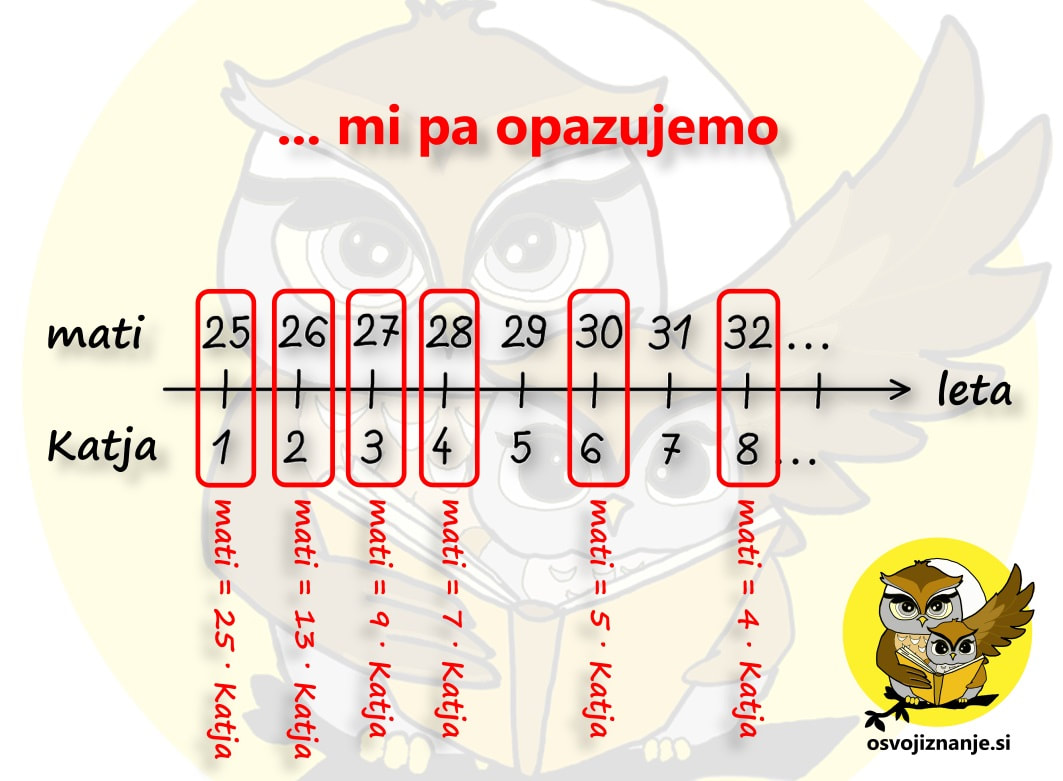
Poanta nalog o starosti je, da isto stvar zapišemo na dva (neodvisna) načina (enkrat »na plus« in enkrat »na krat«), nato pa rešimo sistem enačb in rešitev je tu. Sliši se enostavno, ampak ... je res? In kje v enačbi je časovni stroj? Pojdimo lepo po vrsti. Najprej poglejmo na situacijo pasivno. Dejstvo je, da leta tečejo vsem enako in vsi smo vsako leto eno leto starejši. S tem ni prizanešeno niti našim junakom besedilnih nalog o starosti. V našem primeru sta to mati in njena hči Katja. Za lažjo predstavo naj čas teče v desno, kot smo navajeni s pouka fizike. Starost matere lahko opazujemo na zgornji strani časovne osi, starost Katje pa na spodnji. Sedaj pa prenehajmo z lenarjenjem in zaženimo časovni stroj. :) V časovnem stroju nas pa ne zanima, kako tečejo leta, saj lahko ta trenutek v pradavnini bežimo pred dinozavri, par sekund kasneje pa preizkušamo svoj novi leteči avtomobil. Nas pa v vsakem letu "pristanka" zanima soodvisnost med nastopajočimi, konkretno kolikoKRAT je nekdo starejši od drugega. Ko smo v nekem letu, nas ne zanima preteklost in prihodnost, ukvarjamo se zgolj s podatki, ki jih imamo v danem trenutku (v določenem letu) na voljo. Na kratko ponovimo "recept":
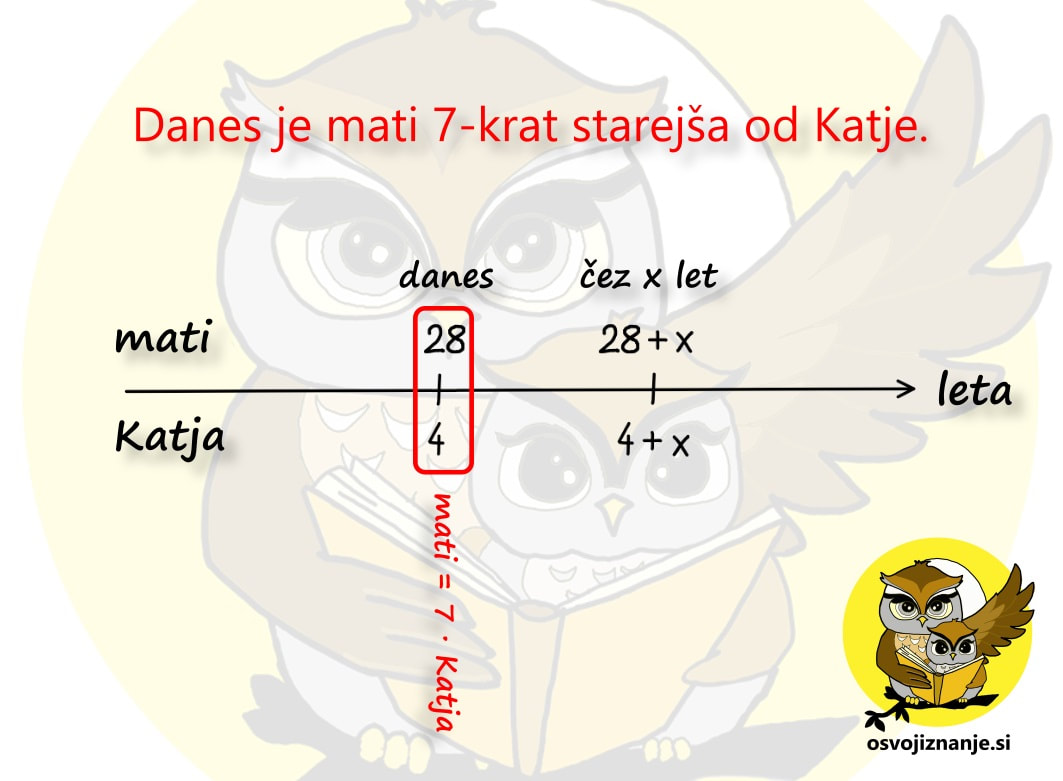
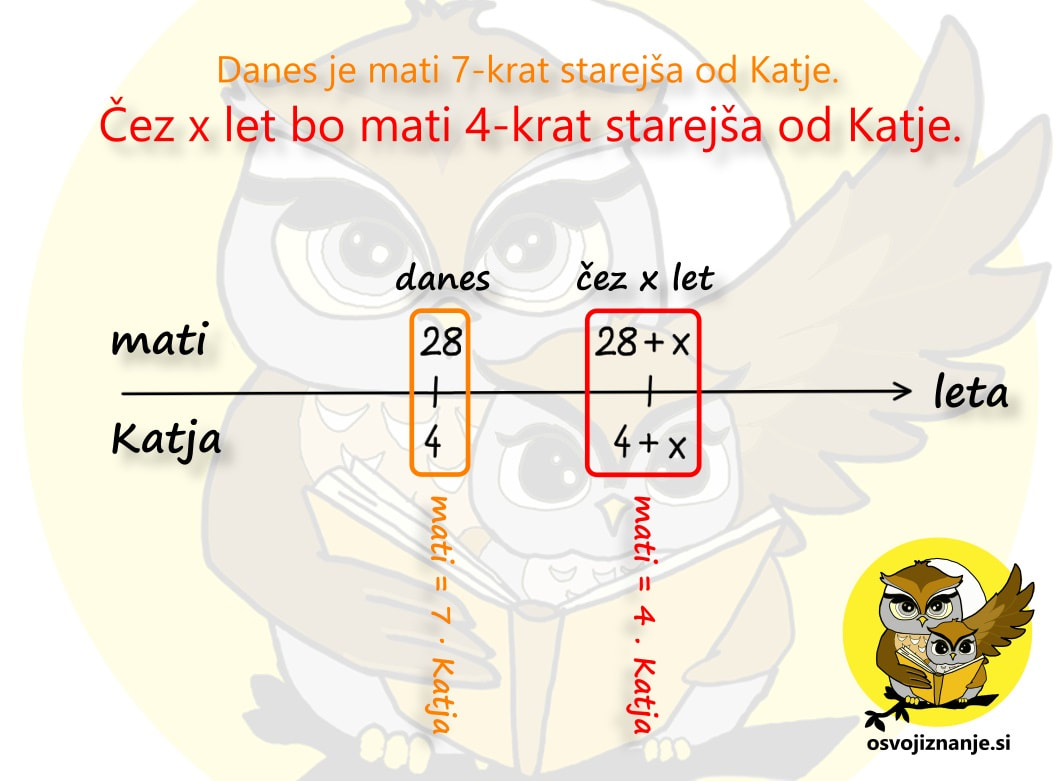
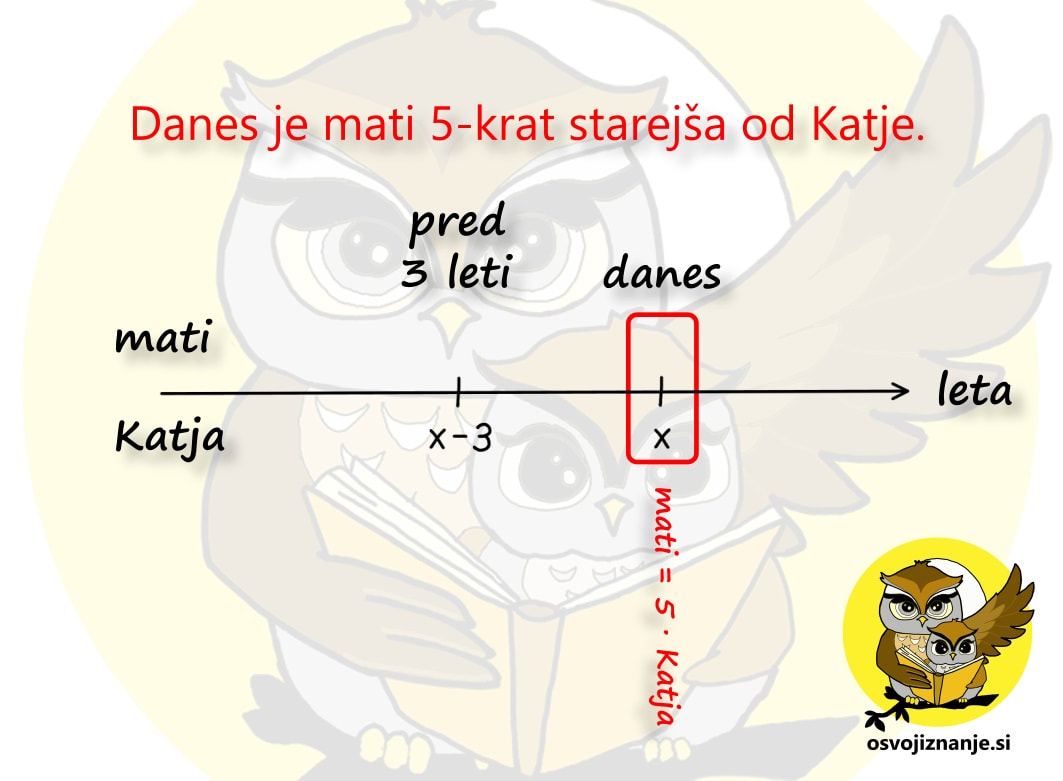
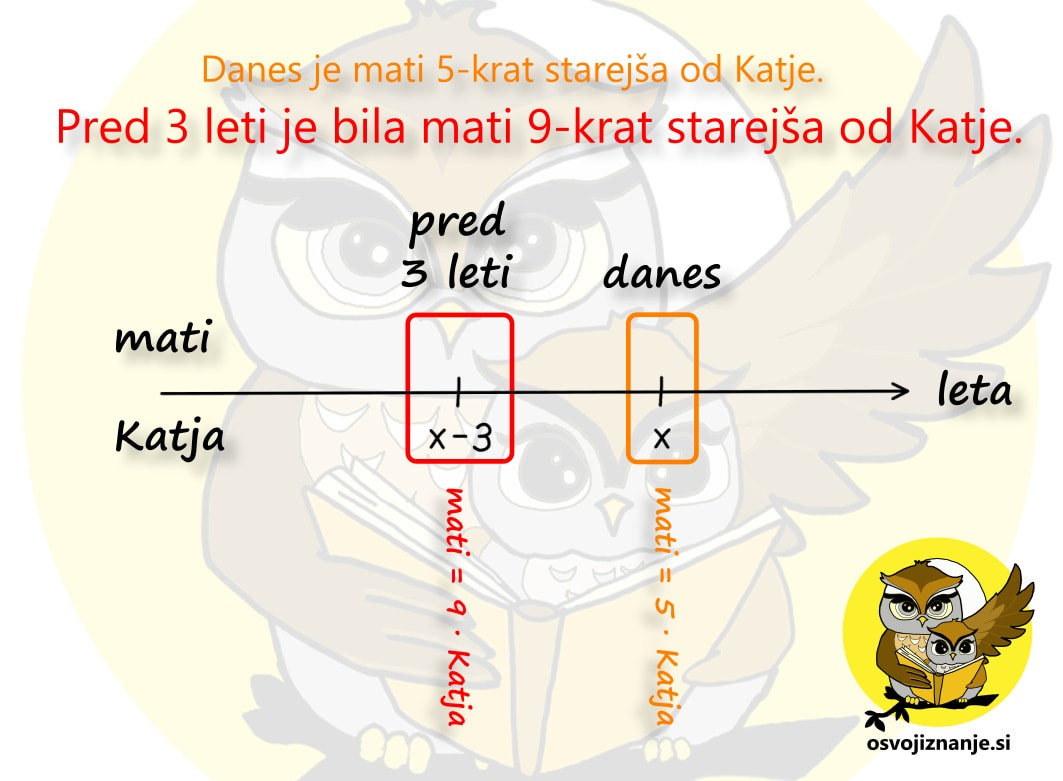
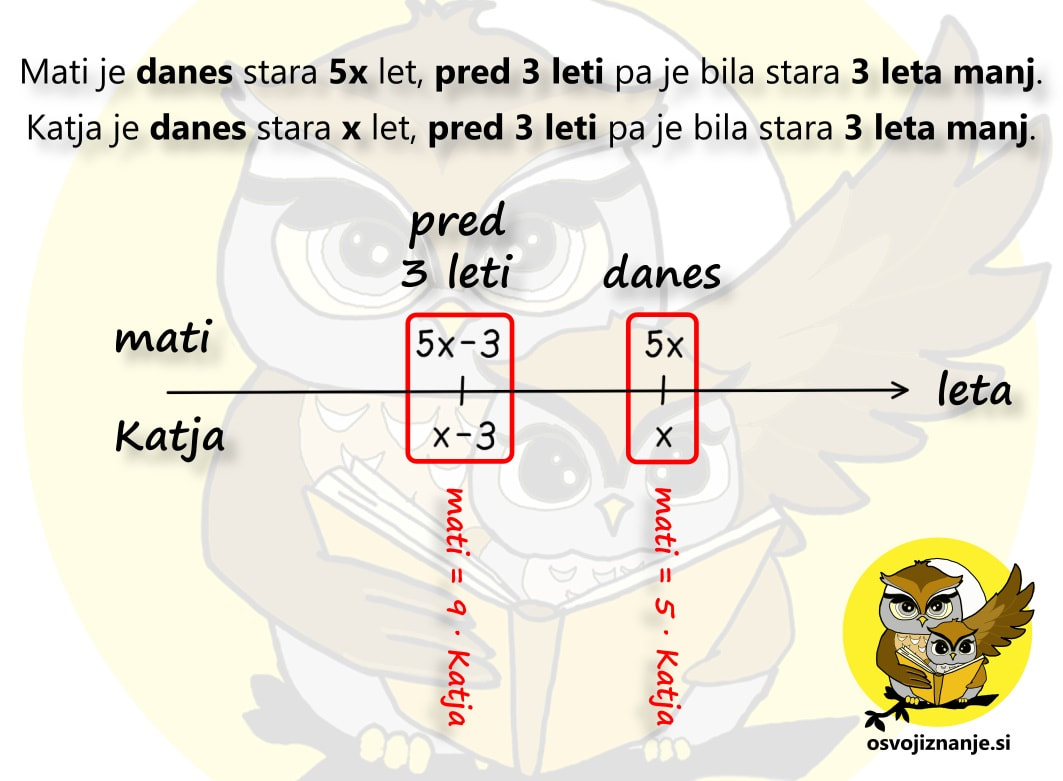
Pa še ena stvar je pomembna pri nalogah o starosti - podatek, ki manjka, označimo z x. To je lahko število pretečenih let ali pa starost katerega od nastopajočih. A pazimo: z neznanko x ne označujmo "skritega" podatka, ki je določljiv z enostavnim računom poštevanke ali seštevanja / odštevanja (npr. starost 6-krat starejšega očeta, če je sin star 5 let - v takem primeru kar pogumno zapišimo, da je oče star 6 x 5 = 30 let). Oglejmo si dva primera nalog o starosti. Naloga 1: Katja je danes stara 4 leta, njena mati pa je 7-krat starejša. Čez koliko let bo mati samo še 4x starejša od Katje? Narišimo časovno os in označimo najprej znane količine. Katja je danes stara 4 leta, starost matere pa lahko določimo posredno iz podatka, da je mati 7-krat starejša od Katje. 7 krat 4 je 28, torej je danes mati stara 28 let. Starost matere danes je v našem primeru "skriti" podatek. Naloga nas sprašuje o dogodku, ki se bo zgodil v preteklosti ("čez koliko let bo ..."). Kot vemo, leta tečejo in mi se staramo. Tudi Katja in njena mati bosta čez nekaj let starejši. Ker ne vemo, koliko let bosta starejši, označimo število pretečenih let z neznanko x. »Po matematično« starost Katje čez x let označimo s 4+x, starost njene matere pa z 28+x. Opomba: Če bi se vprašanje v nalogi nanašalo na preteklost, bi x odšteli. Povezavo levo-desno (seštevanje oz. odštevanje) smo torej obdelali, sedaj pa se usedimo v časovni stroj in preverimo še navpično povezavo. Preden »poletimo«, še enkrat preverimo, kolikokrat je v sedanjosti mati starejša od Katje in to označimo na časovni osi: Wruuum! In smo že v prihodnosti. Točneje, x let v prihodnosti, ko je mati stara 28+x, Katja pa 4+x let. Zopet se osredotočimo na navpično povezavo, kjer nas zanima to, kolikokrat je eden starejši od drugega. In v letu »danes + x« velja, da je mati 4-krat starejša od Katje. Označimo na grafu še to: Obe povezavi levo-desno in obe navpični povezavi imamo, preostane nam le še končni račun. Danes velja enačba Mati = 7 · Katja. Preverimo, če drži. Če za starost matere vzamemo vrednost 28, za starost Katje pa 4, dobimo račun 28=7·4, ki je pravilen. Če danes velja Mati = 7 · Katja, mora v prihodnosti veljati tudi Mati = 4 · Katja, saj tako pravi besedilo naloge. V enačbo vstavimo starost matere in katje čez x let in dobimo: 28 + x = 4·(4+x) 28 + x = 16 + 4x 3 x = 12 x = 4 Ker je x enak 4, pomeni, da smo s časovnim strojem potovali x let v prihodnost. Še preverimo, da se pri računanju nismo zmotili. Čez 4 leta bo Katja stara 4+4=8 let, njena mati pa 28+4=32, kar je res 4-krat več od Katje. Naloga 2: Mati je 5-krat starejša od Katje, pred tremi leti pa je bila 9-krat starejša od nje. Koliko sta stari? Narišimo časovno os in označimo najprej znane količine. Tokrat ne poznamo nobene starosti, vemo le, da med enim in drugim dogodkom pretečejo 3 leta. Zato moramo eno od starosti poimenovati z x, ostale pa bomo zapisali v relativni obliki. Najlažje bo, če z x označimo leta mlajše osebe v sedanjosti. Katja je mlajša, zato je danes stara x let, pred tremi leti pa je bila 3 leta mlajša, torej je bila stara x-3 let. Povezavo levo-desno za Katjo torej imamo. Kaj pa mati? Za to pa se bo potrebno usesti v časovni stroj. Preden »poletimo« (3 leta) v preteklost, preverimo, kolikokrat je v sedanjosti mati starejša od Katje in to označimo na časnovni osi. Mati je 5-krat starejša od Katje, torej velja mati = 5 · Katja: Sedaj pa poletimo 3 leta v preteklost in še tam poglejmo, kolikokrat je mati starejša od Katje. 9-krat, torej velja mati = 9 · Katja: Sedaj imamo dve navpični povezavi (danes in pred 3 leti), manjka pa nam še povezava levo-desno za mati. Ker smo x že uporabili za Katjo, bomo za mater uporabili večkratnik x, najbolje kar v tistem časovnem obdobju, ko ima Katja x, torej v sedanjosti. Danes je mati 5-krat starejša od Katje, torej je stara 5x let. Ker se stara enako kot Katja, pa je bila pred 3 leti stara 3 leta manj, torej 5x-3 let. Tudi to označimo na grafu: Obe povezavi levo-desno in obe navpični povezavi torej imamo, preostane nam le še končni račun.
Danes velja enačba mati = 5 · Katja. Če vanjo vstavimo materina in Katjina leta, se enačba glasi 5x = 5·x, kar je sicer pravilno, pomaga nam pa ne prav dosti. :) K sreči imamo dve enačbi še 3 leta v preteklosti. V tistem času velja mati = 9 · Katja. Ko vanjo vstavimo materina in Katjina leta (pred 3 leti, seveda), se enačba glasi: 5x-3= 9·(x-3) 5x – 3 = 9x – 27 4x = 24 x=6 Ker je x enak 6, pomeni, je Katja danes stara 6 let. Koliko je stara mati? 5-krat starejša je od Katje, torej je stara 5x6=30 let. Še preverimo, da se pri računanju nismo zmotili. Pred 3 leti je bila Katja stara 6-3=3 leta, mati pa 30-3=27 let, kar je res 9-krat več od Katje.
0 Comments
Tale tip besedilnih nalog je marsikomu kar dobro poznan, bodisi zato, ker take naloge rad rešuje, bodisi zato, ker je "alergičen nanje". :) Metod za reševanje le-teh je veliko, meni so bolj všeč bolj sistematične. Naj vam eno predstavim, najlažje kar na primeru: Besedilo smo obarvali po naslednjem ključu:
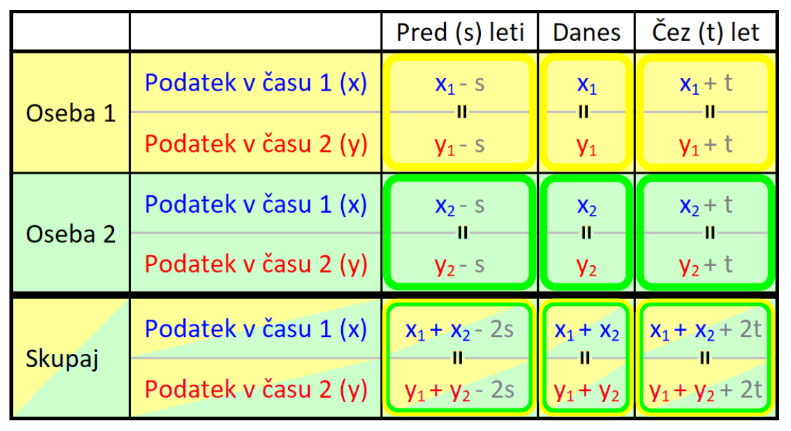
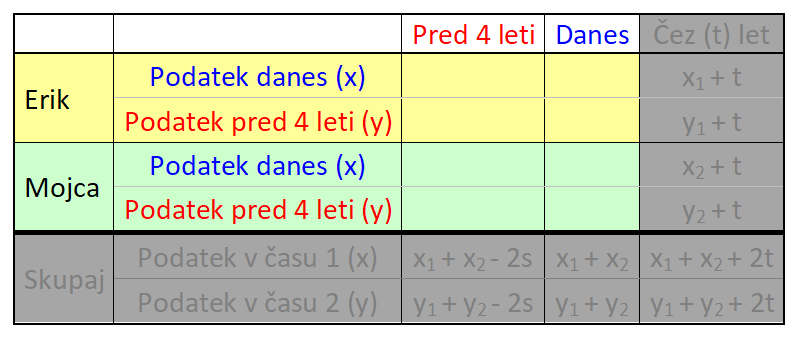
Vprašanje zaenkrat še pustimo, k njem se vrnemo pri interpretaciji rezultata. Pri reševanju naloge bomo uporabili naslednjo (univerzalno) tabelo, v kateri so:
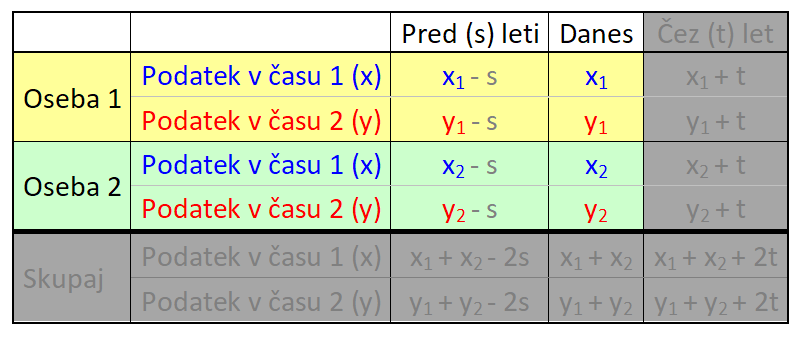
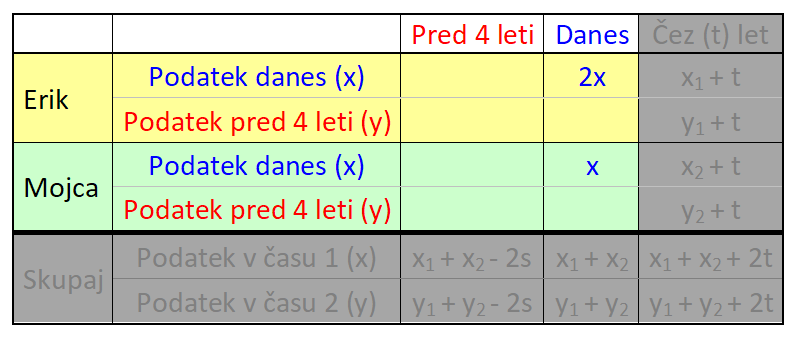
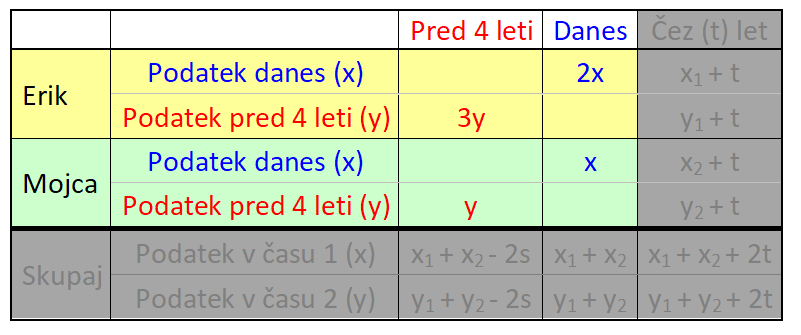
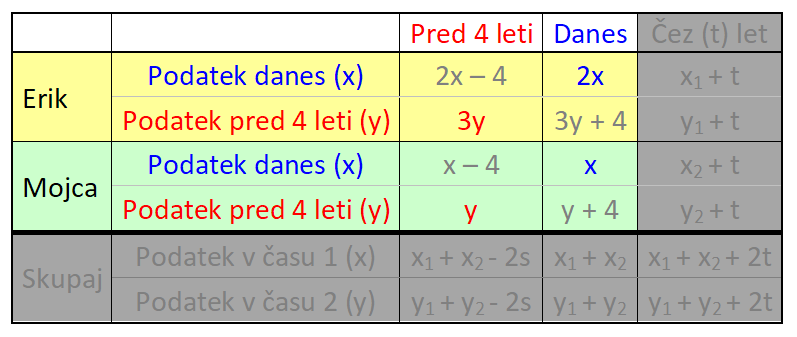
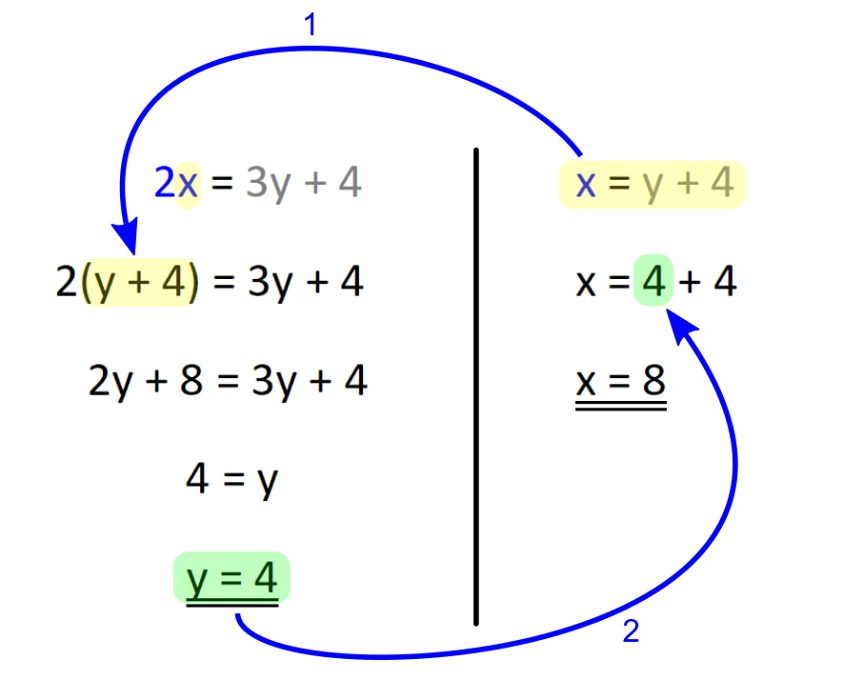
V našem primeru gre za dogajanje v preteklosti in sedanjosti, zato bomo uporabili le prvi in drugi stolpec. V nalogi nastopata dve osebi in sicer vsaka posebej, zato zadnje vrstice prav tako ne bomo potrebovali: V tabelo vnesemo imena in časovne podatke, del s splošnimi spremenljivkami pa izbrišemo, vanj bomo v nadaljevanju korak za korakom vnesli konkretne vrednosti. V tabelo vnesemo podatek za čas 1 (v našem prumeru sedanjost). Ker je Erik dvakrat starejši od Mojce, za Erika zapišemo 2x, za Mojco pa x: Nato v tabelo vnesemo podatek za čas 2 (v našem primeru 4 leta nazaj). Ker je bil pred štirimi leti Erik trikrat starejši od Mojce, za Erika zapišemo 3y, za Mojco pa y: Kot vidimo, je za vsak čas "rezervirana" ena spremenljivka. Danes x, pred 4 leti y. To dvoje moramo vedno ločevati; če bomo na primer zapisali tako v rdeča kot modra polja x, bo izračun napačen. Sedaj dopolnimo še manjkajoča polja v tabeli. Razmišljamo logično, recimo: če je danes Erik star 2x let, je bil pred 4 leti star 4 leta manj, torej 2x-4. Poenostavljeno rečeno - če dopolnjujemo v desno, prištejemo razliko v letih med enim in drugim časom, če pa dopolnjujemo v levo, pa jo odštejemo. V našem primeru je razlika 4 leta. Sledi nastavljanje sistema enačb. Zanj potebujemo eno enačbo iz "rumenega polja" in eno iz "zelenega polja". Enačbi "enake barve" namreč nista neodvisni, zato z njima ne moremo računati (imata neskončno rešitev). Pri odločitvi imamo povsem proste roke - izberemo take enačbe, ki jih bomo lažje rešili. Jaz sem izbral naslednji: Pri nastavljanju sistema enačb si lahko pomagamo z univerzalno tabelo, ki smo jo spoznali na začetku tega prispevka. Rešimo sistem enačb. X iz prve enačbe vstavimo v drugo in izračunamo y, nato pa y vstavimo nazaj v prvo enačbo in dobimo še x: Na koncu pa še zelo pomembno opravilo - interpretacija rezultata.
V našem primeru nas zanima, koliko sta Erik in Mojca stara danes, zato gledamo desni stolpec v tabeli (danes). Vsako polje v tabeli je razdeljeno na zgornji in spodnji del, za katerega vemo, da sta enaka, zato rešitev preberemo iz tistega, ki ima »manj zakompliciran« zapis: |
Arhiv
December 2023
kategorije
All
|





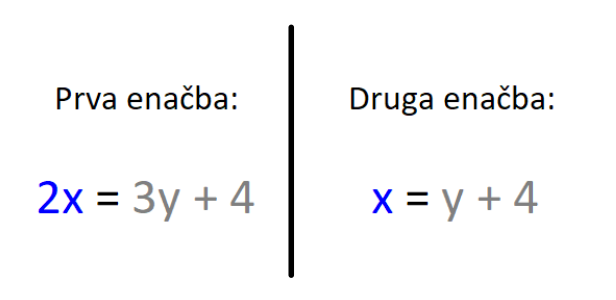
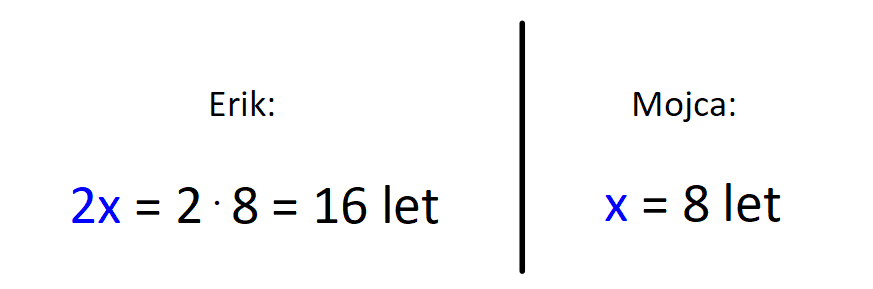
 RSS Feed
RSS Feed
