|
Tale tip besedilnih nalog je marsikomu kar dobro poznan, bodisi zato, ker take naloge rad rešuje, bodisi zato, ker je "alergičen nanje". :) Metod za reševanje le-teh je veliko, meni so bolj všeč bolj sistematične. Naj vam eno predstavim, najlažje kar na primeru: Besedilo smo obarvali po naslednjem ključu:
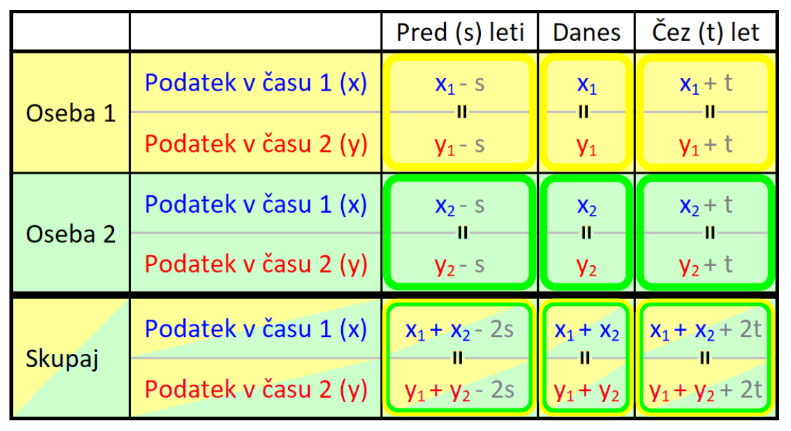
Vprašanje zaenkrat še pustimo, k njem se vrnemo pri interpretaciji rezultata. Pri reševanju naloge bomo uporabili naslednjo (univerzalno) tabelo, v kateri so:
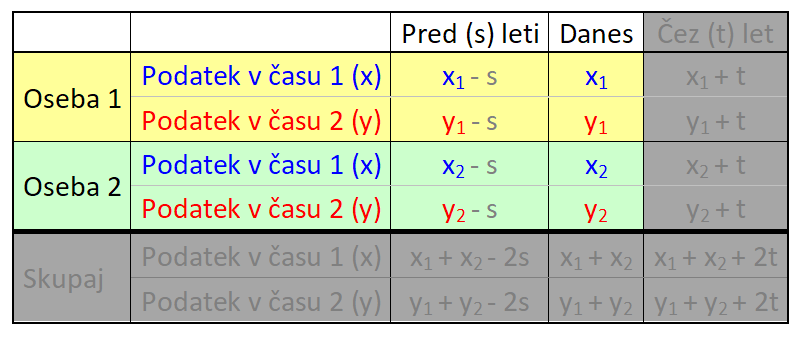
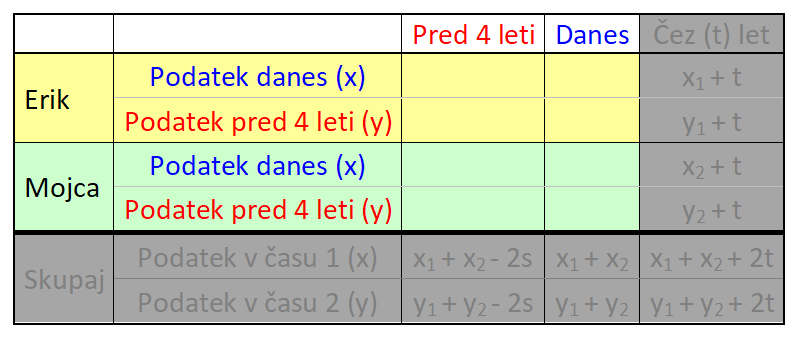
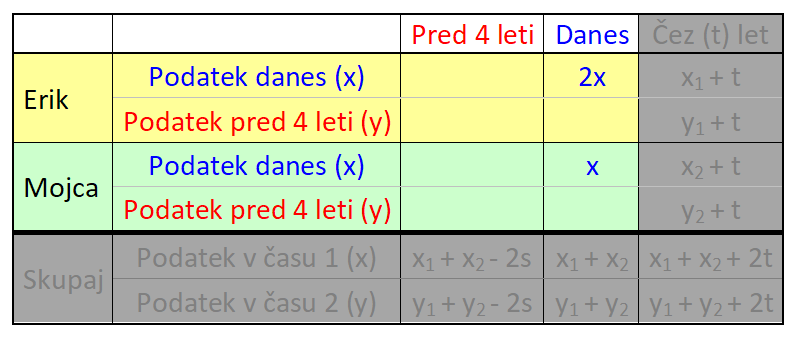
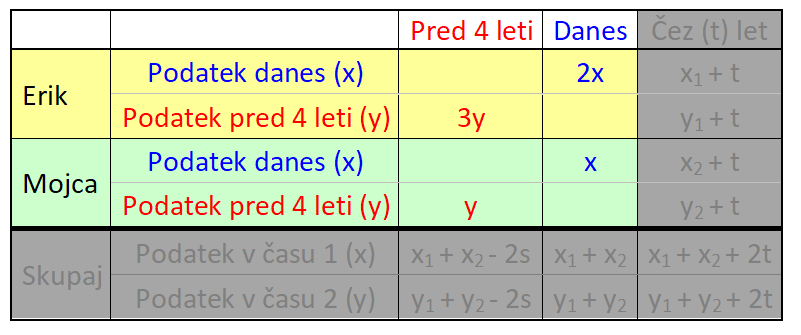
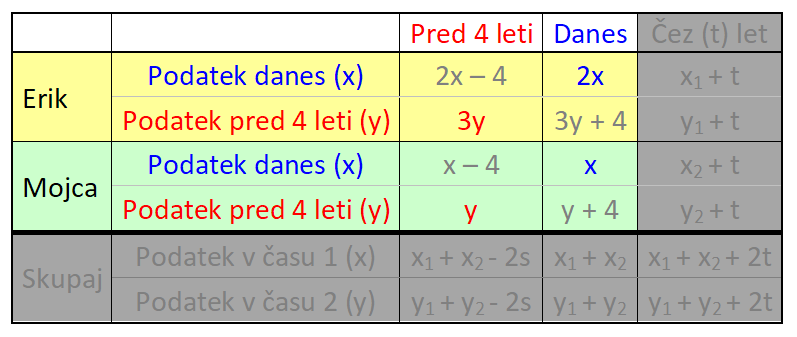
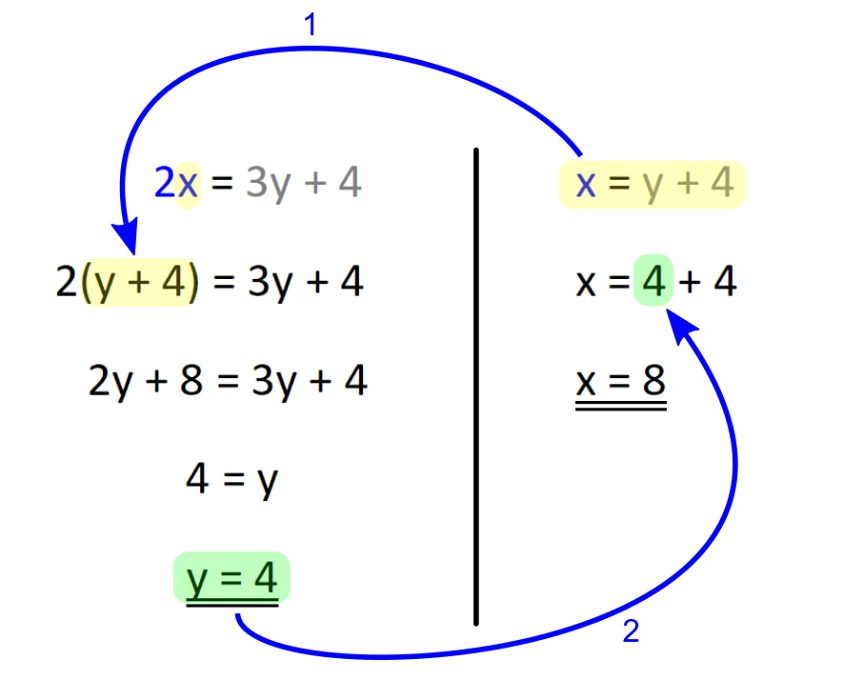
V našem primeru gre za dogajanje v preteklosti in sedanjosti, zato bomo uporabili le prvi in drugi stolpec. V nalogi nastopata dve osebi in sicer vsaka posebej, zato zadnje vrstice prav tako ne bomo potrebovali: V tabelo vnesemo imena in časovne podatke, del s splošnimi spremenljivkami pa izbrišemo, vanj bomo v nadaljevanju korak za korakom vnesli konkretne vrednosti. V tabelo vnesemo podatek za čas 1 (v našem prumeru sedanjost). Ker je Erik dvakrat starejši od Mojce, za Erika zapišemo 2x, za Mojco pa x: Nato v tabelo vnesemo podatek za čas 2 (v našem primeru 4 leta nazaj). Ker je bil pred štirimi leti Erik trikrat starejši od Mojce, za Erika zapišemo 3y, za Mojco pa y: Kot vidimo, je za vsak čas "rezervirana" ena spremenljivka. Danes x, pred 4 leti y. To dvoje moramo vedno ločevati; če bomo na primer zapisali tako v rdeča kot modra polja x, bo izračun napačen. Sedaj dopolnimo še manjkajoča polja v tabeli. Razmišljamo logično, recimo: če je danes Erik star 2x let, je bil pred 4 leti star 4 leta manj, torej 2x-4. Poenostavljeno rečeno - če dopolnjujemo v desno, prištejemo razliko v letih med enim in drugim časom, če pa dopolnjujemo v levo, pa jo odštejemo. V našem primeru je razlika 4 leta. Sledi nastavljanje sistema enačb. Zanj potebujemo eno enačbo iz "rumenega polja" in eno iz "zelenega polja". Enačbi "enake barve" namreč nista neodvisni, zato z njima ne moremo računati (imata neskončno rešitev). Pri odločitvi imamo povsem proste roke - izberemo take enačbe, ki jih bomo lažje rešili. Jaz sem izbral naslednji: Pri nastavljanju sistema enačb si lahko pomagamo z univerzalno tabelo, ki smo jo spoznali na začetku tega prispevka. Rešimo sistem enačb. X iz prve enačbe vstavimo v drugo in izračunamo y, nato pa y vstavimo nazaj v prvo enačbo in dobimo še x: Na koncu pa še zelo pomembno opravilo - interpretacija rezultata.
V našem primeru nas zanima, koliko sta Erik in Mojca stara danes, zato gledamo desni stolpec v tabeli (danes). Vsako polje v tabeli je razdeljeno na zgornji in spodnji del, za katerega vemo, da sta enaka, zato rešitev preberemo iz tistega, ki ima »manj zakompliciran« zapis:
0 Comments
Leave a Reply. |
Arhiv
December 2023
kategorije
All
|

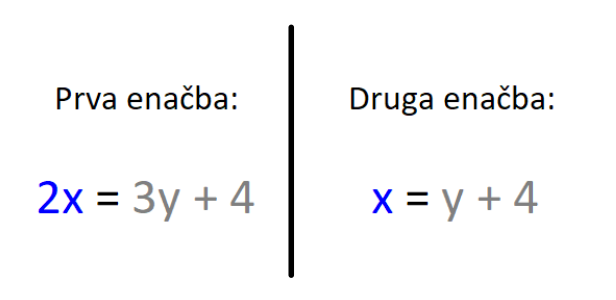
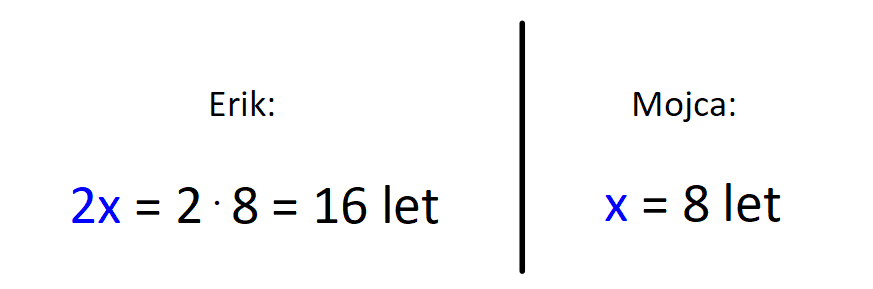
 RSS Feed
RSS Feed
