|
Metod za reševanje besedilnih nalog je celo morje, nekaj jih najdete tudi na blogu, strokovnjaki pa vedno bolj priporočajo t.i. problemski pristop k reševanju, saj so v tem primeru naši možgani najbolj zaposleni in gradijo največ matematičnih povezav.
Tudi pri »igranju s številkami« imamo na voljo več strategij, najbolje pa se obnese tista, ki jo na podlagi predznanja in izkušenj »izumimo« sami. Ob reševanju vsake besedilne naloge v naših možganih namreč zgradimo kar nekaj novih povezav (no, točneje se to dogaja med spanjem, ampak več o tem ob kakšni drugi priložnosti), ki jih kasneje lahko koristno uporabimo. Včasih pomaga, če si besedilno nalogo zgolj poenostavimo, da bi lažje razumeli samo bistvo le-te. Če nismo obremenjeni s »prevelikimi« ali »zakompliciranimi« številkami (na primer takimi s petimi decimalnimi mesti), imamo v delovnem spominu več prostora za razmišljanje o tem, kako bi nalogo rešili. Primer: Ana ima prihranjenih 582,35 EUR, Marko 472,65 EUR, Katja pa 502,33 EUR. Kdo je prihranil največ in kdo najmanj? Kolikšna je razlika med največjim in najmanjšim zneskom? Namesto velikih števil lahko uporabimo manjše, pri čemer upoštevamo razliko njihovih velikosti. Ana ima največ, nato Katja, najmanj ima Marko. Namesto »zakompliciranih« zneskov lahko rečemo, da ima Ana 3 evre, Katja 2, Marko pa 1 EUR. Tu hitro vidimo, da je razlika med Aninim in Markotovim zneskom 2 EUR, račun se glasi 3-1=2. Če sedaj uporabimo »velike« številke, dobimo račun 582,35-472,65. Rezultat pa je naš odgovor. Nalogo si lahko še dodatno poenostavimo z uporabo izrazov »več«, »manj« in »enako« namesto konkretnih števil. Tudi vprašanje za začetek lahko »postavimo na stranski tir«. Tako se res osredotočimo le na razumevanje problema in se ne obremenjujemo z računanjem, vsaj na začetku ne. Kogar zanima še kaj več na to temo, si lahko ogleda naslednji povezavi:
0 Comments
Tale tip besedilnih nalog je marsikomu kar dobro poznan, bodisi zato, ker take naloge rad rešuje, bodisi zato, ker je "alergičen nanje". :) Metod za reševanje le-teh je veliko, meni so bolj všeč bolj sistematične. Naj vam eno predstavim, najlažje kar na primeru: Besedilo smo obarvali po naslednjem ključu:
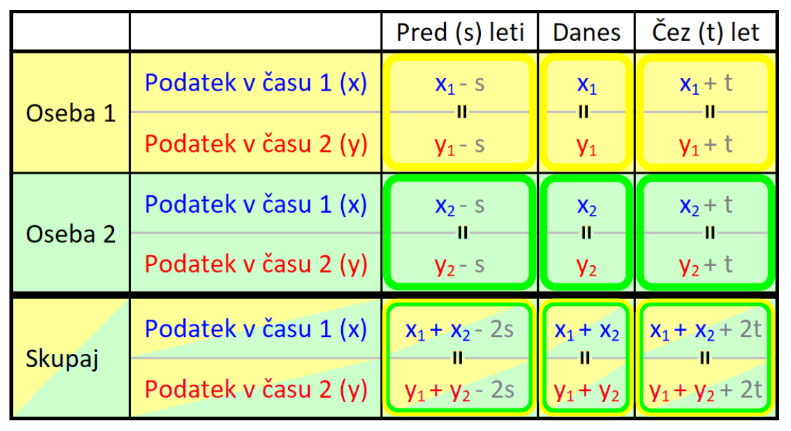
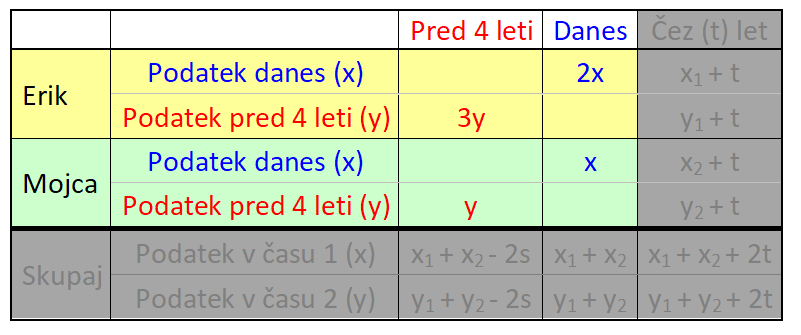
Vprašanje zaenkrat še pustimo, k njem se vrnemo pri interpretaciji rezultata. Pri reševanju naloge bomo uporabili naslednjo (univerzalno) tabelo, v kateri so:
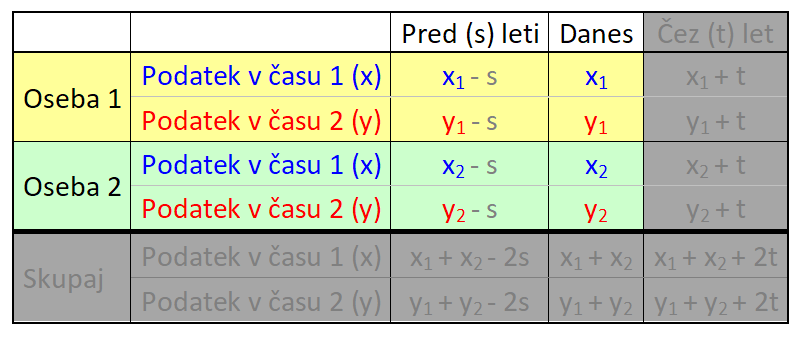
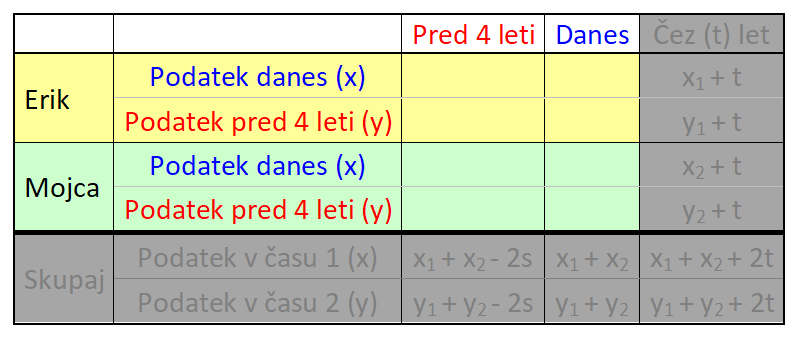
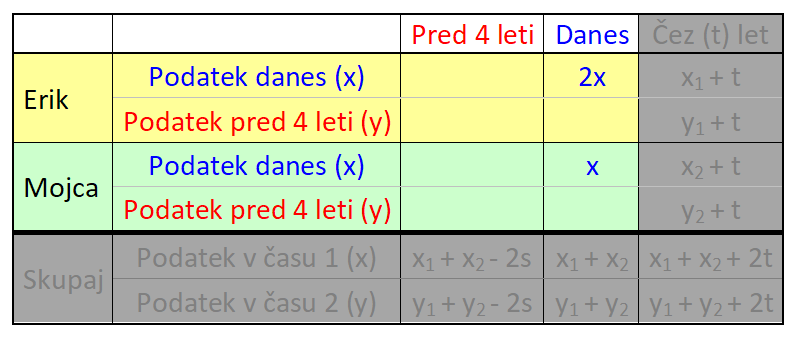
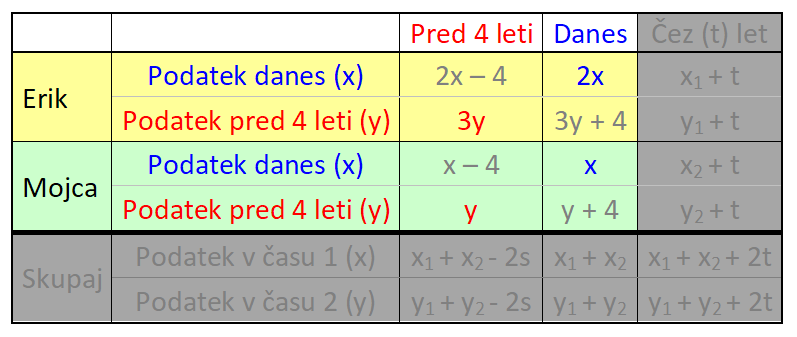
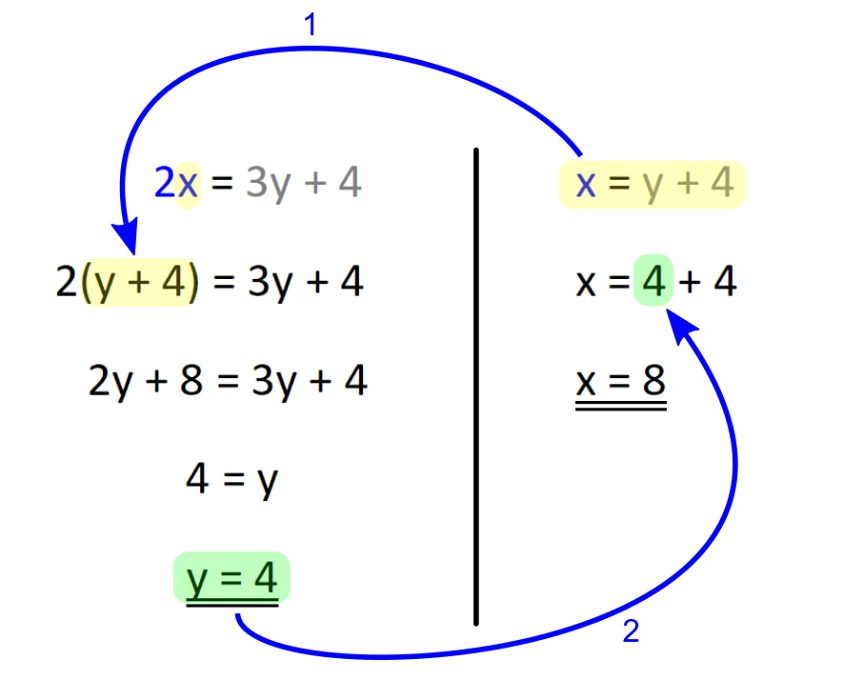
V našem primeru gre za dogajanje v preteklosti in sedanjosti, zato bomo uporabili le prvi in drugi stolpec. V nalogi nastopata dve osebi in sicer vsaka posebej, zato zadnje vrstice prav tako ne bomo potrebovali: V tabelo vnesemo imena in časovne podatke, del s splošnimi spremenljivkami pa izbrišemo, vanj bomo v nadaljevanju korak za korakom vnesli konkretne vrednosti. V tabelo vnesemo podatek za čas 1 (v našem prumeru sedanjost). Ker je Erik dvakrat starejši od Mojce, za Erika zapišemo 2x, za Mojco pa x: Nato v tabelo vnesemo podatek za čas 2 (v našem primeru 4 leta nazaj). Ker je bil pred štirimi leti Erik trikrat starejši od Mojce, za Erika zapišemo 3y, za Mojco pa y: Kot vidimo, je za vsak čas "rezervirana" ena spremenljivka. Danes x, pred 4 leti y. To dvoje moramo vedno ločevati; če bomo na primer zapisali tako v rdeča kot modra polja x, bo izračun napačen. Sedaj dopolnimo še manjkajoča polja v tabeli. Razmišljamo logično, recimo: če je danes Erik star 2x let, je bil pred 4 leti star 4 leta manj, torej 2x-4. Poenostavljeno rečeno - če dopolnjujemo v desno, prištejemo razliko v letih med enim in drugim časom, če pa dopolnjujemo v levo, pa jo odštejemo. V našem primeru je razlika 4 leta. Sledi nastavljanje sistema enačb. Zanj potebujemo eno enačbo iz "rumenega polja" in eno iz "zelenega polja". Enačbi "enake barve" namreč nista neodvisni, zato z njima ne moremo računati (imata neskončno rešitev). Pri odločitvi imamo povsem proste roke - izberemo take enačbe, ki jih bomo lažje rešili. Jaz sem izbral naslednji: Pri nastavljanju sistema enačb si lahko pomagamo z univerzalno tabelo, ki smo jo spoznali na začetku tega prispevka. Rešimo sistem enačb. X iz prve enačbe vstavimo v drugo in izračunamo y, nato pa y vstavimo nazaj v prvo enačbo in dobimo še x: Na koncu pa še zelo pomembno opravilo - interpretacija rezultata.
V našem primeru nas zanima, koliko sta Erik in Mojca stara danes, zato gledamo desni stolpec v tabeli (danes). Vsako polje v tabeli je razdeljeno na zgornji in spodnji del, za katerega vemo, da sta enaka, zato rešitev preberemo iz tistega, ki ima »manj zakompliciran« zapis: |
Arhiv
December 2023
kategorije
All
|


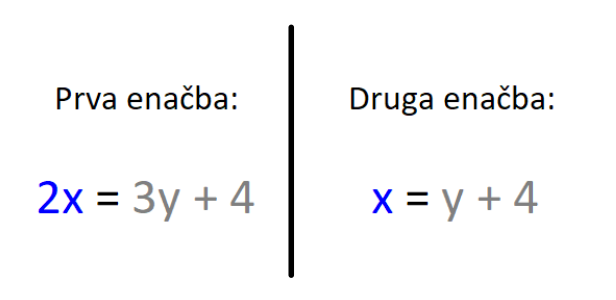
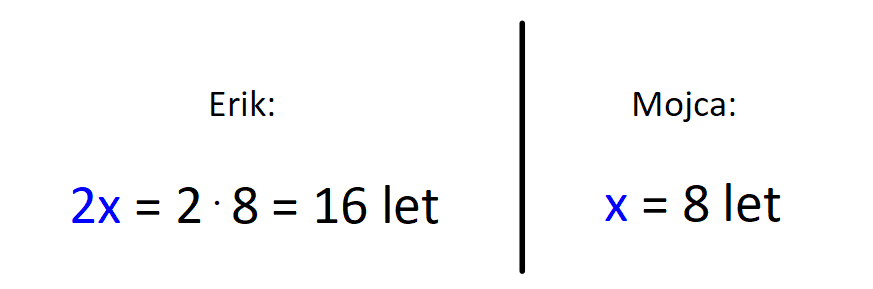
 RSS Feed
RSS Feed
