|
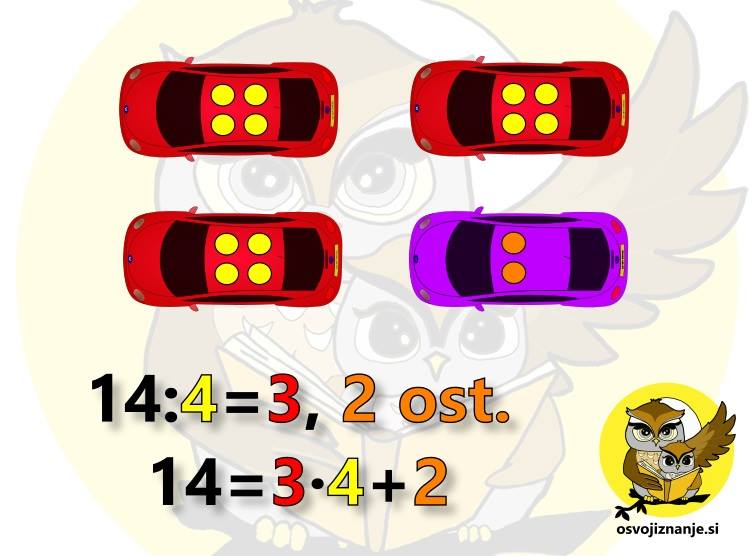
Marsikatero besedilno nalogo lahko rešimo že z enostavnim premislekom. glejmo si dve taki nalogi, pri katerih uporabimo deljenje z ostankom. Z najmanj koliko avtomobili se lahko pelje 14 oseb, če se v enem avtu lahko peljejo največ štiri osebe? 14 ljudi bomo razdelili v skupine po 4, zato zapišemo račun 14:4. Rezultat deljenja je 3, ostanek pa 2. Kaj nam pove rezultat? 14 ljudi torej lahko razdelimo v 3 skupine po 4 (3 krat 4 je 12), dva pa "ostaneta zunaj". Za preostala dva človeka moramo torej "naročiti" še en avto, skupaj torej potrebujemo 4. A le trije bodo polni, v zadnjem bosta sedela le dva. Še dobro, da imamo na voljo dovolj avtomobilov, sicer bi zadnja dva morala iti kar peš ;) Do konca knjige nam je preostalo še 89 strani. Koliko strani moramo prebrati vsak dan, če moramo čez en teden knjigo vrniti v knjižnico? Tu bomo pa 89 strani razdelili na 7 dni (en teden), zato zapišemo račun 89:7. Rezultat deljenja je 12, ostanek pa 5. Kaj nam pove rezultat? Če 89 strani razdelimo na 7 dni, na vsak dan "odpade" 12 strani, 5 strani pa ostane neprebranih. Ker je knjigo potrebno prebrati v celoti, dodatnega dneva pa si ne moremo privoščiti, je potrebno še preostalih 5 strani "stlačiti" v teh 7 dni. Recimo: od ponedeljka do petka preberemo stran več (12+1), v soboto in nedeljo pa "običajnih" 12. Na ta način smo račun 7⋅12 + 5 "spremenili" v 5⋅13 + 2⋅12, pri čemer se rezultat ne spremeni (= 89). Na koncu naredimo še primerjavo s prejšnjo nalogo. Ker se z enim avtom ne morejo peljati več kot štiri osebe, nihče pa ne želi iti peš 🙂, je nujno potrebno povečati število avtomobilov. Pri današnji nalogi pa v posamezen dan v tednu lahko "stlačimo" še kakšno stran, zato kljub časovni omejitvi lahko knjigo preberemo do konca.
0 Comments
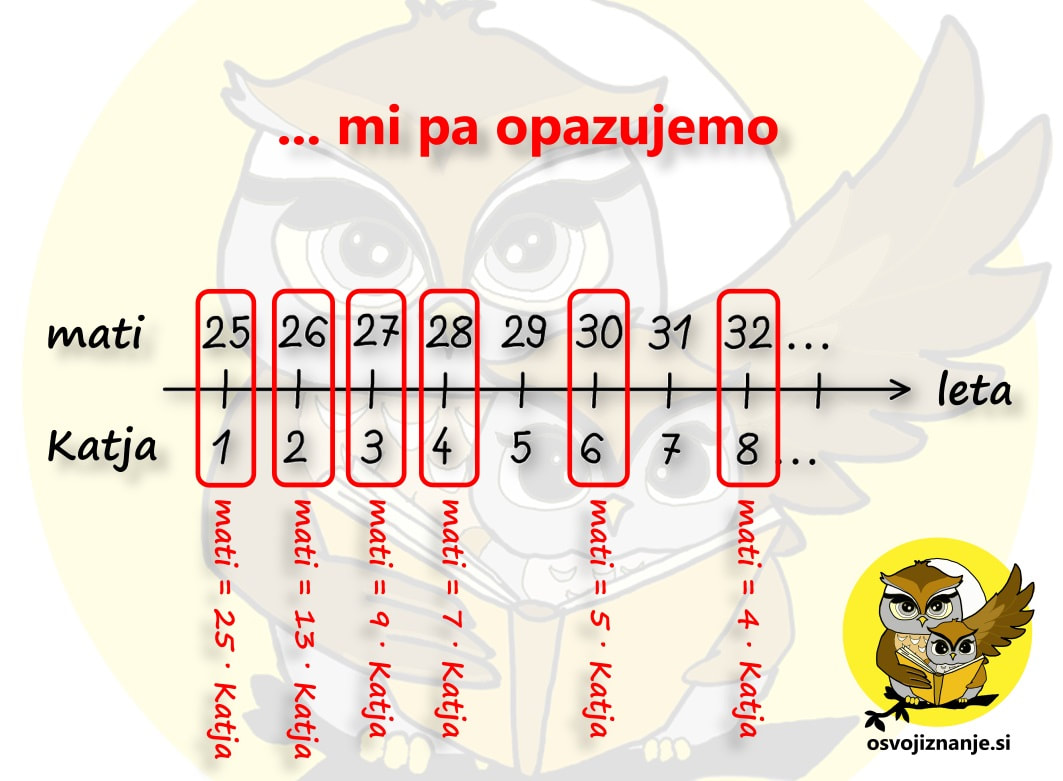
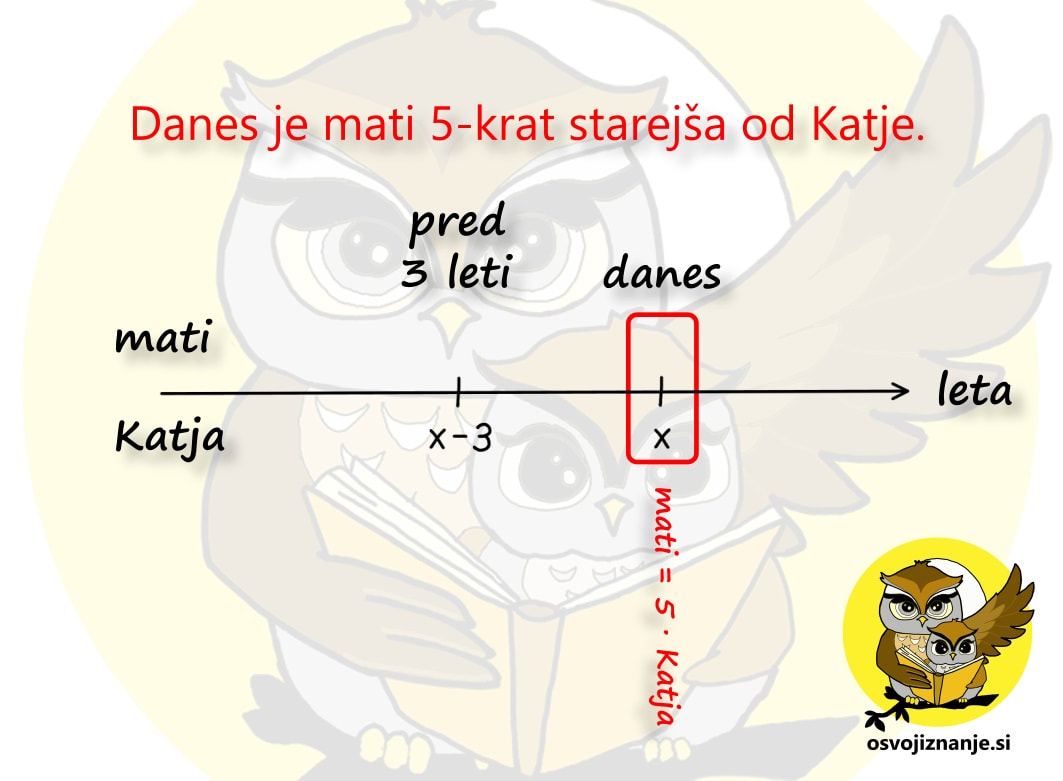
Poanta nalog o starosti je, da isto stvar zapišemo na dva (neodvisna) načina (enkrat »na plus« in enkrat »na krat«), nato pa rešimo sistem enačb in rešitev je tu. Sliši se enostavno, ampak ... je res? In kje v enačbi je časovni stroj? Pojdimo lepo po vrsti. Najprej poglejmo na situacijo pasivno. Dejstvo je, da leta tečejo vsem enako in vsi smo vsako leto eno leto starejši. S tem ni prizanešeno niti našim junakom besedilnih nalog o starosti. V našem primeru sta to mati in njena hči Katja. Za lažjo predstavo naj čas teče v desno, kot smo navajeni s pouka fizike. Starost matere lahko opazujemo na zgornji strani časovne osi, starost Katje pa na spodnji. Sedaj pa prenehajmo z lenarjenjem in zaženimo časovni stroj. :) V časovnem stroju nas pa ne zanima, kako tečejo leta, saj lahko ta trenutek v pradavnini bežimo pred dinozavri, par sekund kasneje pa preizkušamo svoj novi leteči avtomobil. Nas pa v vsakem letu "pristanka" zanima soodvisnost med nastopajočimi, konkretno kolikoKRAT je nekdo starejši od drugega. Ko smo v nekem letu, nas ne zanima preteklost in prihodnost, ukvarjamo se zgolj s podatki, ki jih imamo v danem trenutku (v določenem letu) na voljo. Na kratko ponovimo "recept":
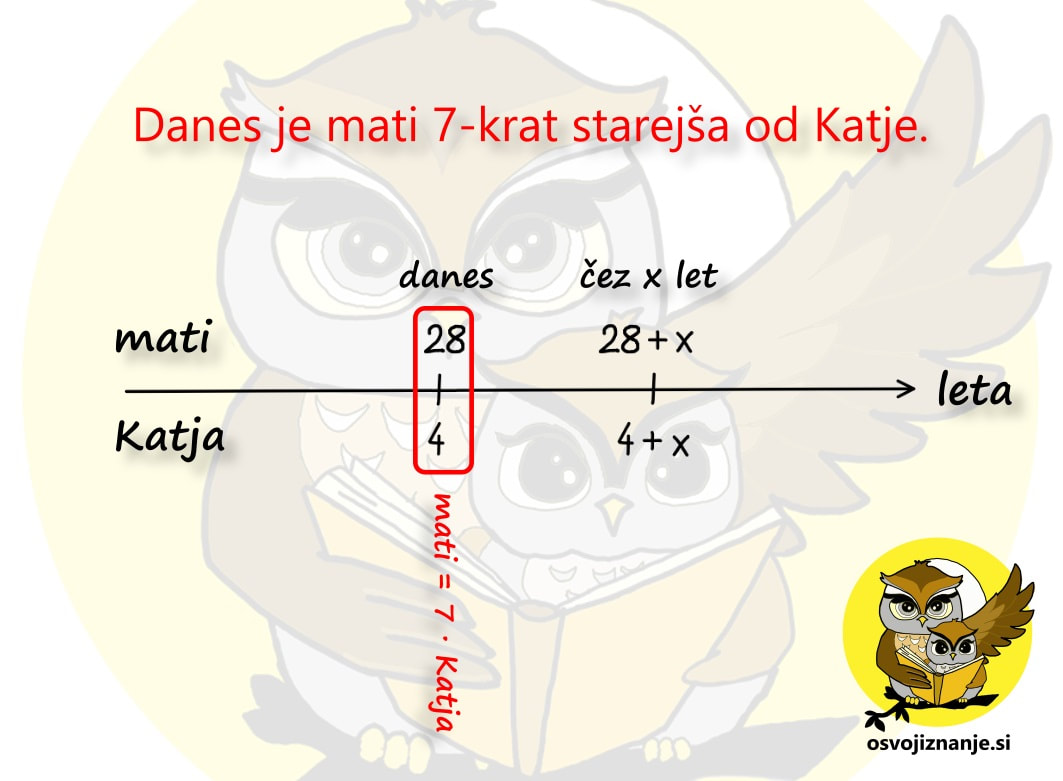
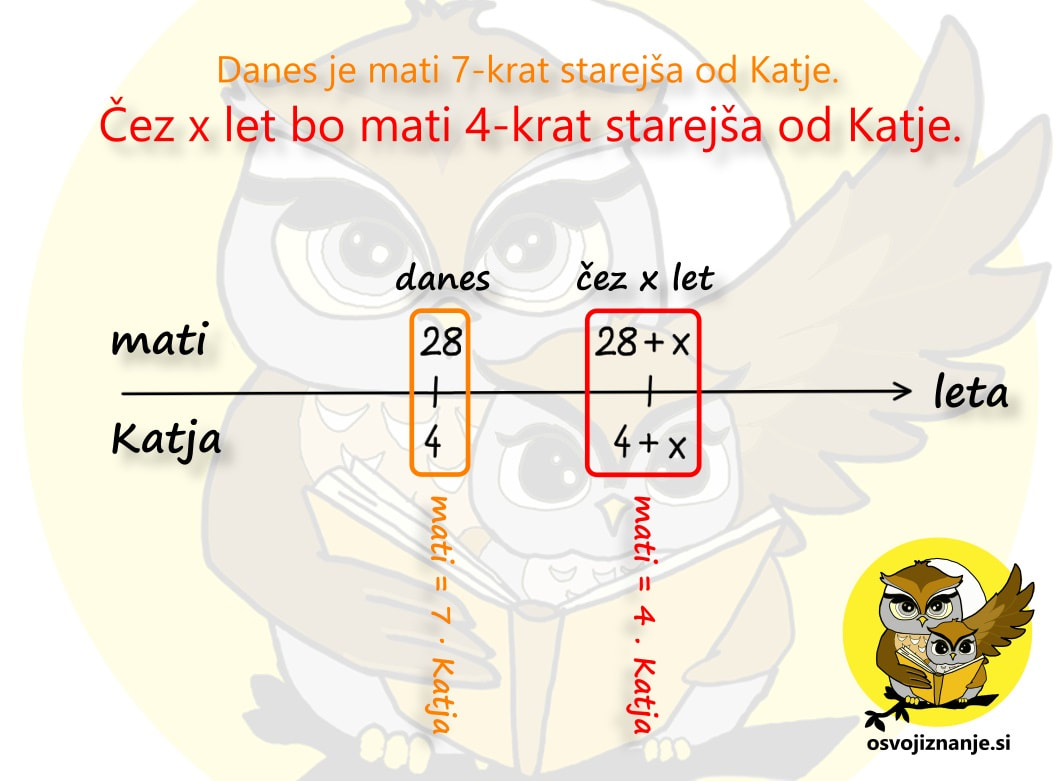
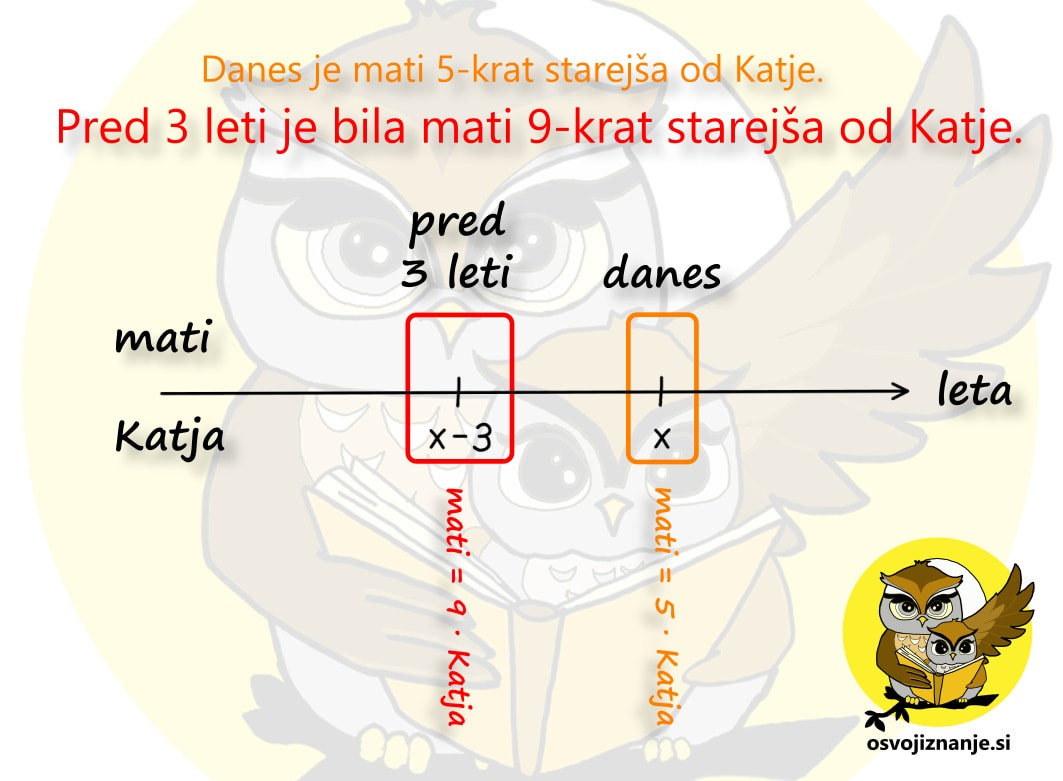
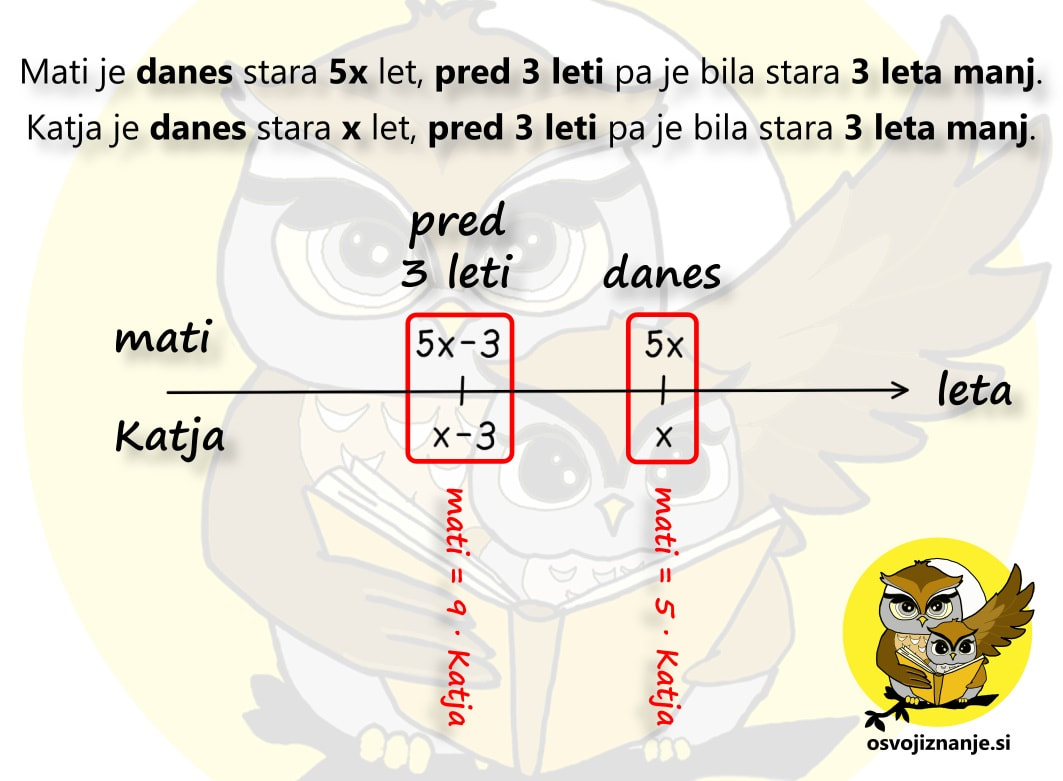
Pa še ena stvar je pomembna pri nalogah o starosti - podatek, ki manjka, označimo z x. To je lahko število pretečenih let ali pa starost katerega od nastopajočih. A pazimo: z neznanko x ne označujmo "skritega" podatka, ki je določljiv z enostavnim računom poštevanke ali seštevanja / odštevanja (npr. starost 6-krat starejšega očeta, če je sin star 5 let - v takem primeru kar pogumno zapišimo, da je oče star 6 x 5 = 30 let). Oglejmo si dva primera nalog o starosti. Naloga 1: Katja je danes stara 4 leta, njena mati pa je 7-krat starejša. Čez koliko let bo mati samo še 4x starejša od Katje? Narišimo časovno os in označimo najprej znane količine. Katja je danes stara 4 leta, starost matere pa lahko določimo posredno iz podatka, da je mati 7-krat starejša od Katje. 7 krat 4 je 28, torej je danes mati stara 28 let. Starost matere danes je v našem primeru "skriti" podatek. Naloga nas sprašuje o dogodku, ki se bo zgodil v preteklosti ("čez koliko let bo ..."). Kot vemo, leta tečejo in mi se staramo. Tudi Katja in njena mati bosta čez nekaj let starejši. Ker ne vemo, koliko let bosta starejši, označimo število pretečenih let z neznanko x. »Po matematično« starost Katje čez x let označimo s 4+x, starost njene matere pa z 28+x. Opomba: Če bi se vprašanje v nalogi nanašalo na preteklost, bi x odšteli. Povezavo levo-desno (seštevanje oz. odštevanje) smo torej obdelali, sedaj pa se usedimo v časovni stroj in preverimo še navpično povezavo. Preden »poletimo«, še enkrat preverimo, kolikokrat je v sedanjosti mati starejša od Katje in to označimo na časovni osi: Wruuum! In smo že v prihodnosti. Točneje, x let v prihodnosti, ko je mati stara 28+x, Katja pa 4+x let. Zopet se osredotočimo na navpično povezavo, kjer nas zanima to, kolikokrat je eden starejši od drugega. In v letu »danes + x« velja, da je mati 4-krat starejša od Katje. Označimo na grafu še to: Obe povezavi levo-desno in obe navpični povezavi imamo, preostane nam le še končni račun. Danes velja enačba Mati = 7 · Katja. Preverimo, če drži. Če za starost matere vzamemo vrednost 28, za starost Katje pa 4, dobimo račun 28=7·4, ki je pravilen. Če danes velja Mati = 7 · Katja, mora v prihodnosti veljati tudi Mati = 4 · Katja, saj tako pravi besedilo naloge. V enačbo vstavimo starost matere in katje čez x let in dobimo: 28 + x = 4·(4+x) 28 + x = 16 + 4x 3 x = 12 x = 4 Ker je x enak 4, pomeni, da smo s časovnim strojem potovali x let v prihodnost. Še preverimo, da se pri računanju nismo zmotili. Čez 4 leta bo Katja stara 4+4=8 let, njena mati pa 28+4=32, kar je res 4-krat več od Katje. Naloga 2: Mati je 5-krat starejša od Katje, pred tremi leti pa je bila 9-krat starejša od nje. Koliko sta stari? Narišimo časovno os in označimo najprej znane količine. Tokrat ne poznamo nobene starosti, vemo le, da med enim in drugim dogodkom pretečejo 3 leta. Zato moramo eno od starosti poimenovati z x, ostale pa bomo zapisali v relativni obliki. Najlažje bo, če z x označimo leta mlajše osebe v sedanjosti. Katja je mlajša, zato je danes stara x let, pred tremi leti pa je bila 3 leta mlajša, torej je bila stara x-3 let. Povezavo levo-desno za Katjo torej imamo. Kaj pa mati? Za to pa se bo potrebno usesti v časovni stroj. Preden »poletimo« (3 leta) v preteklost, preverimo, kolikokrat je v sedanjosti mati starejša od Katje in to označimo na časnovni osi. Mati je 5-krat starejša od Katje, torej velja mati = 5 · Katja: Sedaj pa poletimo 3 leta v preteklost in še tam poglejmo, kolikokrat je mati starejša od Katje. 9-krat, torej velja mati = 9 · Katja: Sedaj imamo dve navpični povezavi (danes in pred 3 leti), manjka pa nam še povezava levo-desno za mati. Ker smo x že uporabili za Katjo, bomo za mater uporabili večkratnik x, najbolje kar v tistem časovnem obdobju, ko ima Katja x, torej v sedanjosti. Danes je mati 5-krat starejša od Katje, torej je stara 5x let. Ker se stara enako kot Katja, pa je bila pred 3 leti stara 3 leta manj, torej 5x-3 let. Tudi to označimo na grafu: Obe povezavi levo-desno in obe navpični povezavi torej imamo, preostane nam le še končni račun.
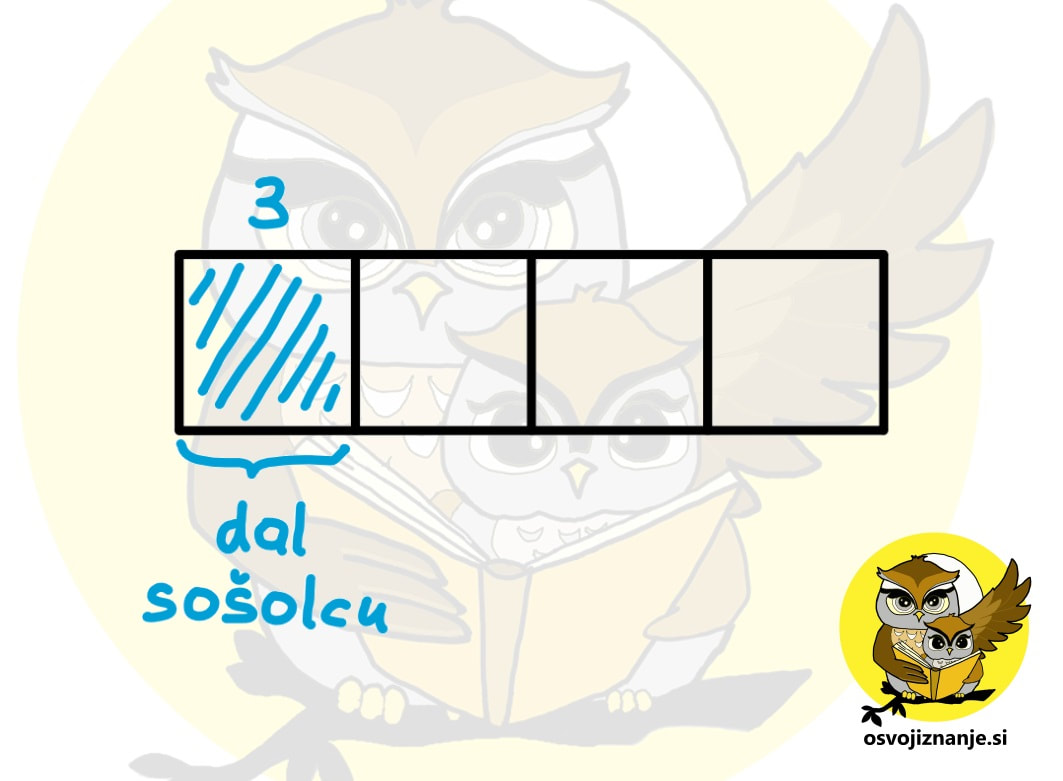
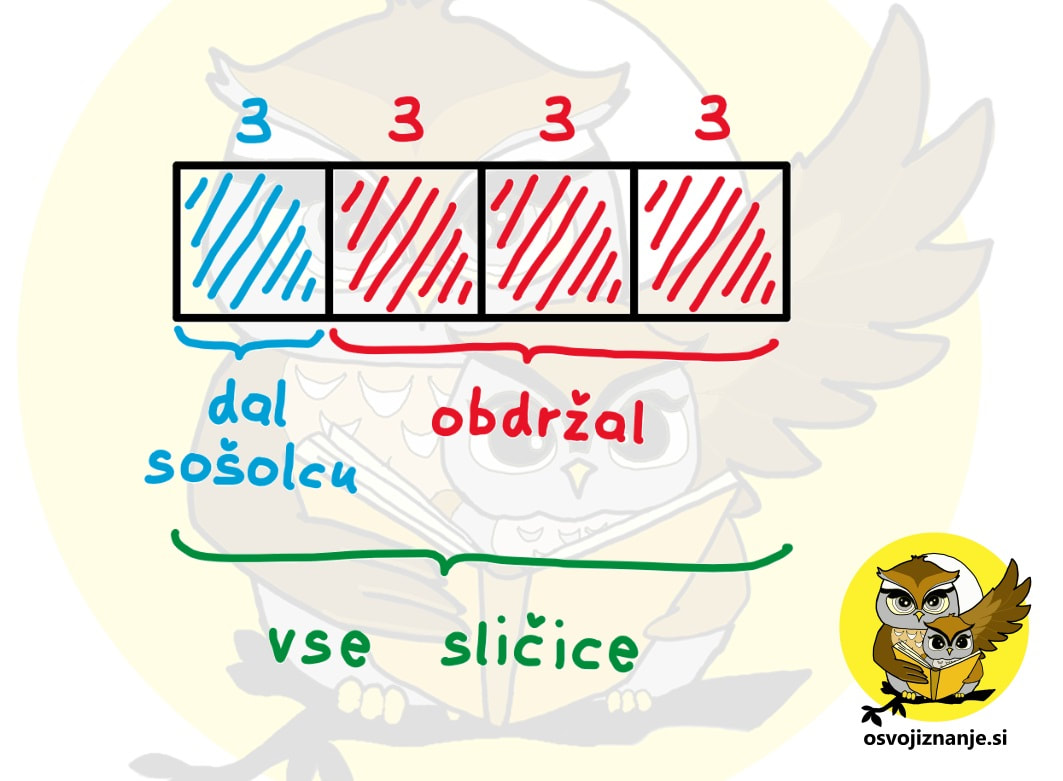
Danes velja enačba mati = 5 · Katja. Če vanjo vstavimo materina in Katjina leta, se enačba glasi 5x = 5·x, kar je sicer pravilno, pomaga nam pa ne prav dosti. :) K sreči imamo dve enačbi še 3 leta v preteklosti. V tistem času velja mati = 9 · Katja. Ko vanjo vstavimo materina in Katjina leta (pred 3 leti, seveda), se enačba glasi: 5x-3= 9·(x-3) 5x – 3 = 9x – 27 4x = 24 x=6 Ker je x enak 6, pomeni, je Katja danes stara 6 let. Koliko je stara mati? 5-krat starejša je od Katje, torej je stara 5x6=30 let. Še preverimo, da se pri računanju nismo zmotili. Pred 3 leti je bila Katja stara 6-3=3 leta, mati pa 30-3=27 let, kar je res 9-krat več od Katje. Kadar v besedilni nalogi nastopajo deleži (1/3, 3/5 ...), si lahko pomagamo z modelom »čokoladne vrstice«. Pa pojdimo v matematične vode, preden nas popade lakota. :) Recimo, da se naloga glasi: »Matej je dal sošolcu 3 sličice, kar znaša četrtino vseh svojih sličic. Koliko sličic je ostalo Mateju?« Čeprav marsikdo nerad riše, še posebej pa pri matematiki, :) se tu splača potruditi. Ko boste problem dejansko videli, ga bo veliko lažje rešiti. Najprej si pripravimo model situacije:
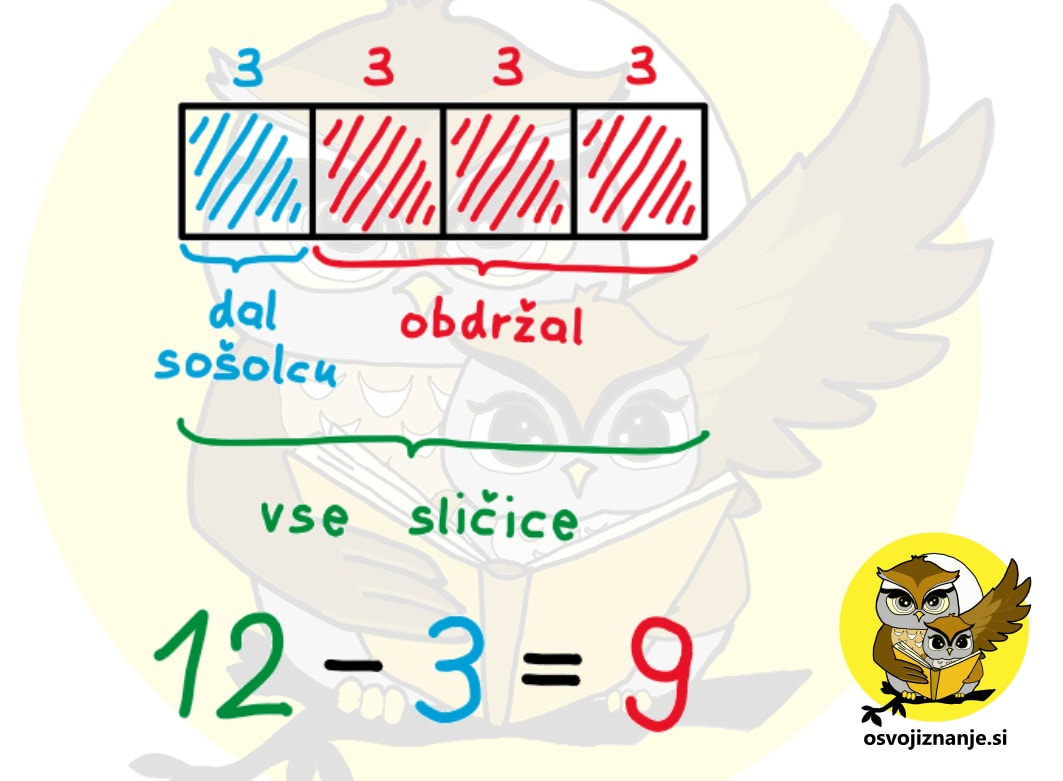
Sedaj pa se malo ustavimo in še preden preberemo vprašanje, si oglejmo problem »od daleč«. Od 4 polj je pobarvano eno in to ima vrednost 3. Ostanejo nam še 3 polja in ker so polja »enakovredna«, imajo tudi ta vrednost 3. Če seštejemo vsa polja, dobimo vrednost 3 + 3 + 3 + 3 = 12, kar pomeni vse sličice – tiste, ki jih je dal in tiste, ki so mu ostale. Nepobarvana polja lahko pobarvamo z drugo barvo (npr. z rdečo) in preštejemo število sličic, ki »spadajo vanje«. To so sličice, ki so Mateju ostale. Če sedaj preberemo, kaj naloga od nas zahteva (vprašanje se glasi: »Koliko sličic je ostalo Mateju?«), vidimo, da imamo odgovor takorekoč na dlani: to je 3 + 3 + 3 = 9 sličic (na skici obarvano rdeče).
Točk na žalost ne bo (po sreči bi jih morda celo pri komu dobili), če ne bo računa. Ampak, ko imamo enkrat pred seboj pregledno skico, tega ni težko zapisati. Od celote (12) odštejemo število oddanih sličic (3) in dobimo 12 – 3 = 9. Metod za reševanje besedilnih nalog je celo morje, nekaj jih najdete tudi na blogu, strokovnjaki pa vedno bolj priporočajo t.i. problemski pristop k reševanju, saj so v tem primeru naši možgani najbolj zaposleni in gradijo največ matematičnih povezav.
Tudi pri »igranju s številkami« imamo na voljo več strategij, najbolje pa se obnese tista, ki jo na podlagi predznanja in izkušenj »izumimo« sami. Ob reševanju vsake besedilne naloge v naših možganih namreč zgradimo kar nekaj novih povezav (no, točneje se to dogaja med spanjem, ampak več o tem ob kakšni drugi priložnosti), ki jih kasneje lahko koristno uporabimo. Včasih pomaga, če si besedilno nalogo zgolj poenostavimo, da bi lažje razumeli samo bistvo le-te. Če nismo obremenjeni s »prevelikimi« ali »zakompliciranimi« številkami (na primer takimi s petimi decimalnimi mesti), imamo v delovnem spominu več prostora za razmišljanje o tem, kako bi nalogo rešili. Primer: Ana ima prihranjenih 582,35 EUR, Marko 472,65 EUR, Katja pa 502,33 EUR. Kdo je prihranil največ in kdo najmanj? Kolikšna je razlika med največjim in najmanjšim zneskom? Namesto velikih števil lahko uporabimo manjše, pri čemer upoštevamo razliko njihovih velikosti. Ana ima največ, nato Katja, najmanj ima Marko. Namesto »zakompliciranih« zneskov lahko rečemo, da ima Ana 3 evre, Katja 2, Marko pa 1 EUR. Tu hitro vidimo, da je razlika med Aninim in Markotovim zneskom 2 EUR, račun se glasi 3-1=2. Če sedaj uporabimo »velike« številke, dobimo račun 582,35-472,65. Rezultat pa je naš odgovor. Nalogo si lahko še dodatno poenostavimo z uporabo izrazov »več«, »manj« in »enako« namesto konkretnih števil. Tudi vprašanje za začetek lahko »postavimo na stranski tir«. Tako se res osredotočimo le na razumevanje problema in se ne obremenjujemo z računanjem, vsaj na začetku ne. Kogar zanima še kaj več na to temo, si lahko ogleda naslednji povezavi: Tale tip besedilnih nalog je marsikomu kar dobro poznan, bodisi zato, ker take naloge rad rešuje, bodisi zato, ker je "alergičen nanje". :) Metod za reševanje le-teh je veliko, meni so bolj všeč bolj sistematične. Naj vam eno predstavim, najlažje kar na primeru: Besedilo smo obarvali po naslednjem ključu:
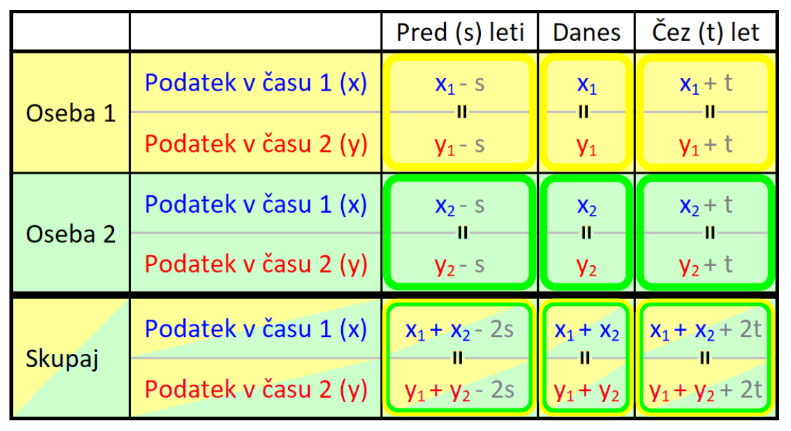
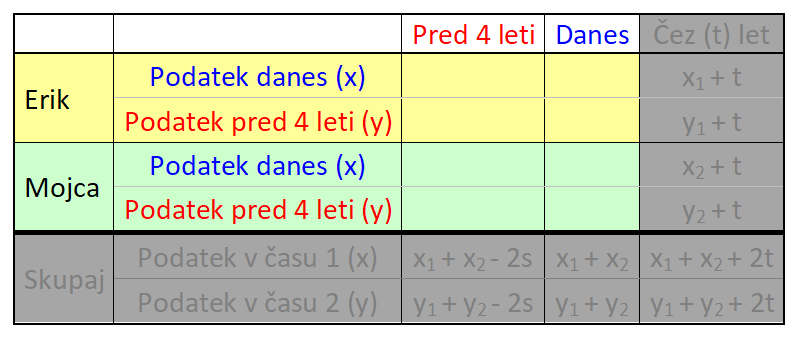
Vprašanje zaenkrat še pustimo, k njem se vrnemo pri interpretaciji rezultata. Pri reševanju naloge bomo uporabili naslednjo (univerzalno) tabelo, v kateri so:
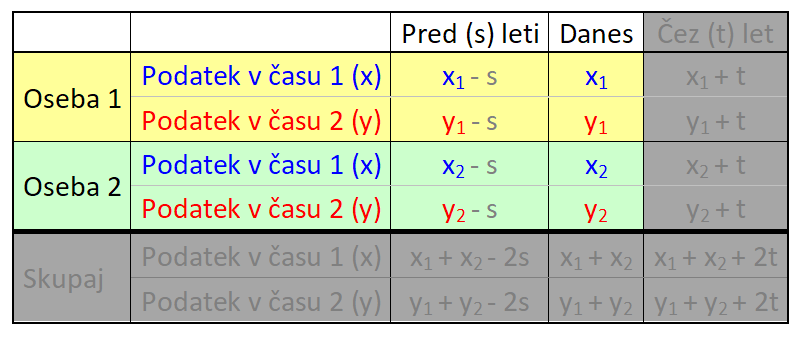
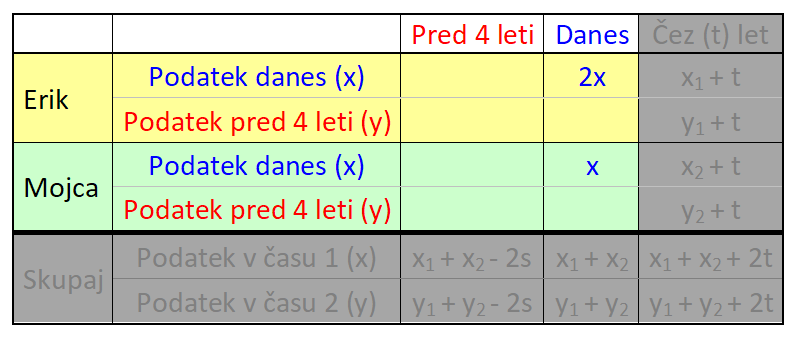
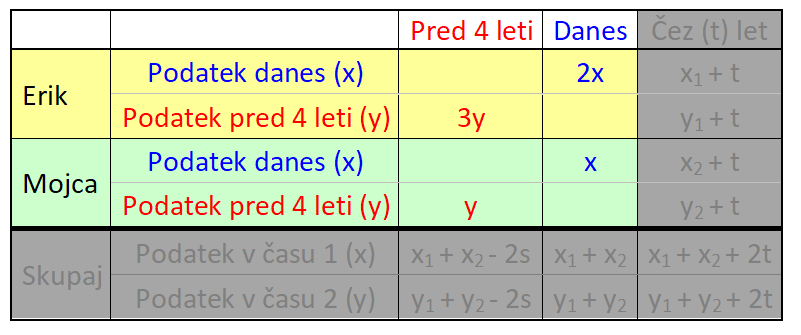
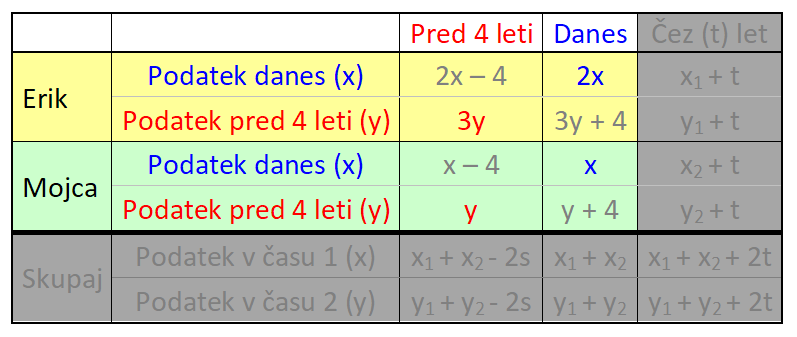
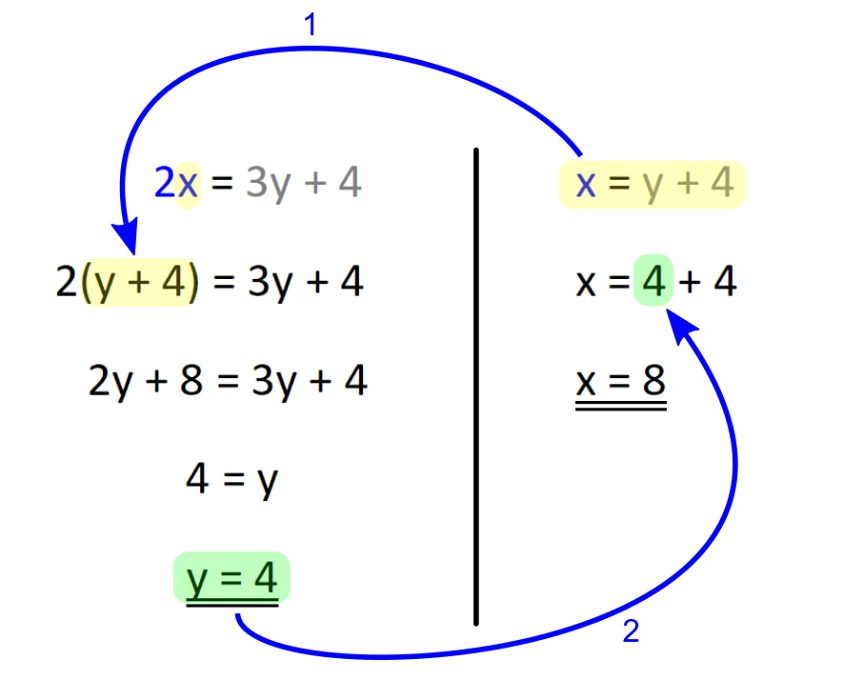
V našem primeru gre za dogajanje v preteklosti in sedanjosti, zato bomo uporabili le prvi in drugi stolpec. V nalogi nastopata dve osebi in sicer vsaka posebej, zato zadnje vrstice prav tako ne bomo potrebovali: V tabelo vnesemo imena in časovne podatke, del s splošnimi spremenljivkami pa izbrišemo, vanj bomo v nadaljevanju korak za korakom vnesli konkretne vrednosti. V tabelo vnesemo podatek za čas 1 (v našem prumeru sedanjost). Ker je Erik dvakrat starejši od Mojce, za Erika zapišemo 2x, za Mojco pa x: Nato v tabelo vnesemo podatek za čas 2 (v našem primeru 4 leta nazaj). Ker je bil pred štirimi leti Erik trikrat starejši od Mojce, za Erika zapišemo 3y, za Mojco pa y: Kot vidimo, je za vsak čas "rezervirana" ena spremenljivka. Danes x, pred 4 leti y. To dvoje moramo vedno ločevati; če bomo na primer zapisali tako v rdeča kot modra polja x, bo izračun napačen. Sedaj dopolnimo še manjkajoča polja v tabeli. Razmišljamo logično, recimo: če je danes Erik star 2x let, je bil pred 4 leti star 4 leta manj, torej 2x-4. Poenostavljeno rečeno - če dopolnjujemo v desno, prištejemo razliko v letih med enim in drugim časom, če pa dopolnjujemo v levo, pa jo odštejemo. V našem primeru je razlika 4 leta. Sledi nastavljanje sistema enačb. Zanj potebujemo eno enačbo iz "rumenega polja" in eno iz "zelenega polja". Enačbi "enake barve" namreč nista neodvisni, zato z njima ne moremo računati (imata neskončno rešitev). Pri odločitvi imamo povsem proste roke - izberemo take enačbe, ki jih bomo lažje rešili. Jaz sem izbral naslednji: Pri nastavljanju sistema enačb si lahko pomagamo z univerzalno tabelo, ki smo jo spoznali na začetku tega prispevka. Rešimo sistem enačb. X iz prve enačbe vstavimo v drugo in izračunamo y, nato pa y vstavimo nazaj v prvo enačbo in dobimo še x: Na koncu pa še zelo pomembno opravilo - interpretacija rezultata.
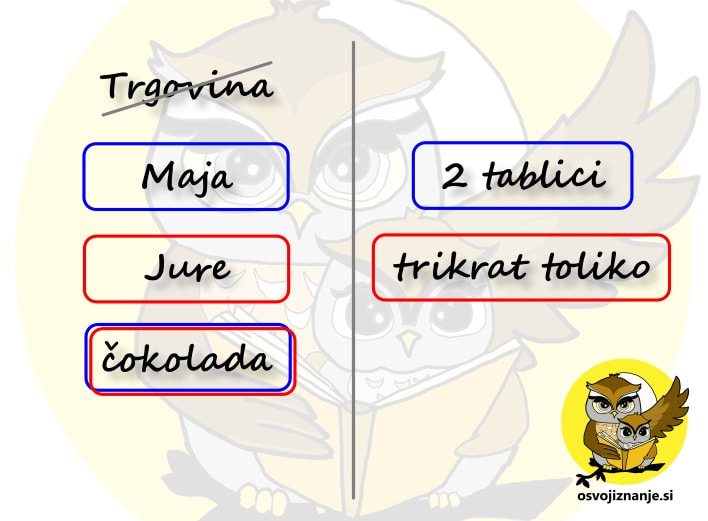
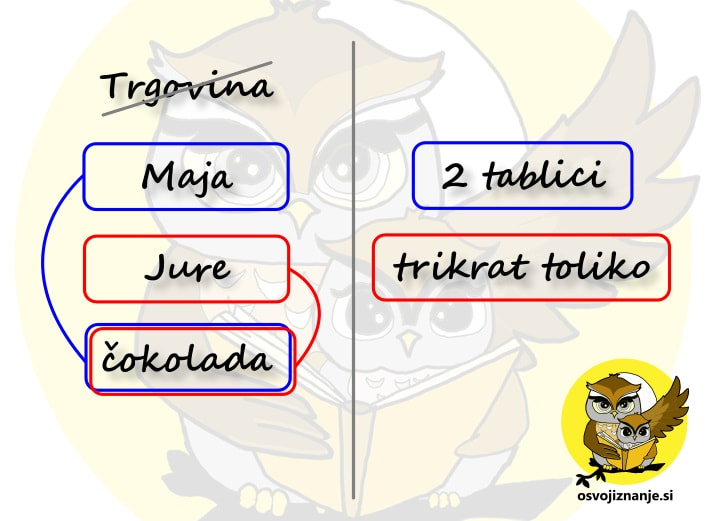
V našem primeru nas zanima, koliko sta Erik in Mojca stara danes, zato gledamo desni stolpec v tabeli (danes). Vsako polje v tabeli je razdeljeno na zgornji in spodnji del, za katerega vemo, da sta enaka, zato rešitev preberemo iz tistega, ki ima »manj zakompliciran« zapis: Za vas imam še eno metodo reševanja besedilnih nalog. Mogoče bo pa ravno ta tista, ki se vam bo dopadla. ;) Seveda si jo lahko tudi po želji prilagodite. V bistvu je to celo zaželjeno. Zadeva je popolnoma preprosta. Naj jo razložim na primeru. Besedilna naloga se glasi: »V trgovini je Maja kupila 2 tablici čokolade, Jure pa trikrat toliko. Koliko čokolade sta kupila oba skupaj?« Pa jo rešimo. Najprej:
Nato z enako barvo obkrožimo vse, kar spada skupaj. Če kakšna oseba oz. predmet nastopa le enkrat, a pripada več skupinam, jo obkrožimo z več barvami. V našem primeru je to čokolada. Če kakšna oseba oz. predmet ni povezana z nobenim podatkom, jo prečrtamo. V našem primeru je to trgovina. Kako vemo, da oseba oz. predmet ni povezana z nobenim podatkom? Možnosti sta (vsaj) dve:
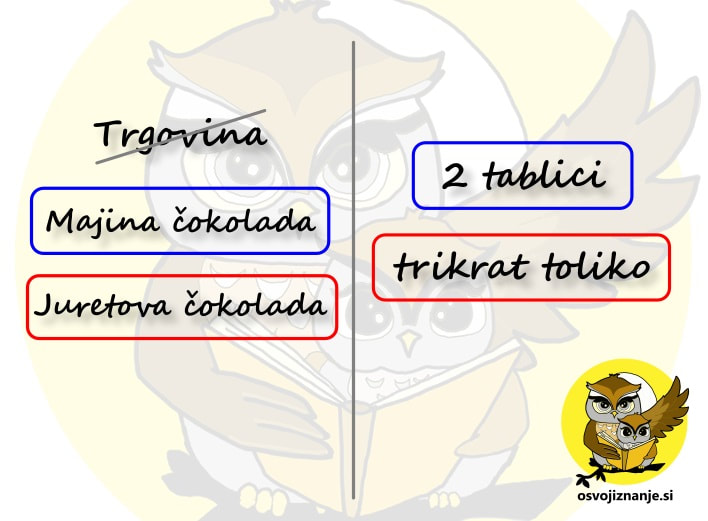
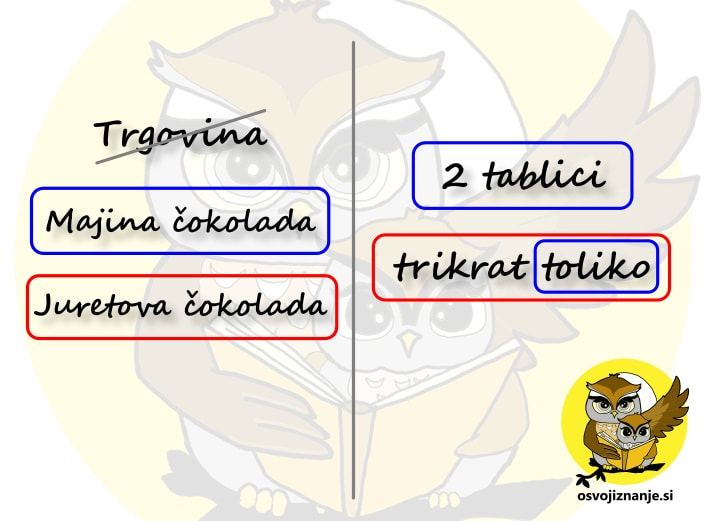
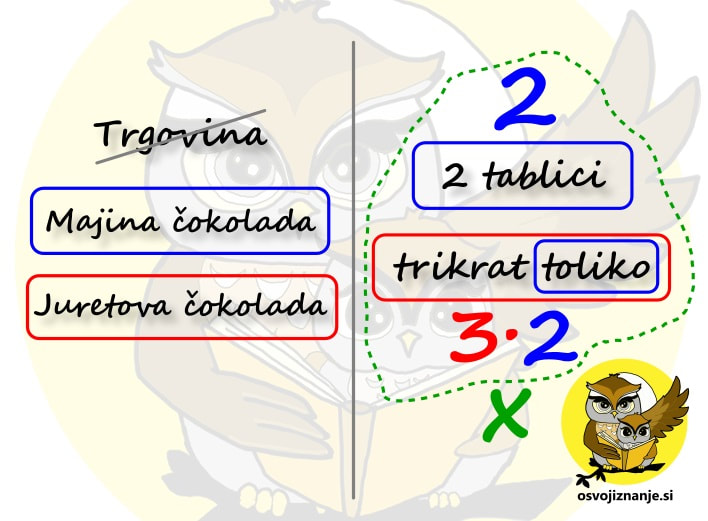
Razmislimo, če z enako barvo obkrožene osebe oz. predmete na levi lahko združimo. Z manj »navlake« bomo lažje nastavili račun. V našem primeru lahko Majo in čokolado združimo v »Majino čokolado«, Jureta in čokolado pa v »Juretovo čokolado«: Sledi zelo pomemben del naloge – poiskati moramo povezavo med podatki. Vsaka besedilna naloga tako povezavo mora vsebovati, sicer je ni možno rešiti. V našem primeru se povezava skriva v besedici »toliko«. Podatek »trikrat toliko« je sicer obarvan rdeče, a besedica »toliko« se nanaša na osebe, predmete in podatke, obarvane modro. Zato besedo »toliko« obkrožimo z modro barvo: Ko imamo vse povezave »pod streho«, si še enkrat oglejmo vprašanje. Kaj moramo izračunati? Ker bomo računali s podatki, se osredotočimo na desno stran lista. V našem primeru nas zanima skupna količina čokolade, torej »moder« in »rdeč« del skupaj. Za še večjo preglednost lahko poleg obkroženih podatkov še na veliko napišemo vrednosti. V našem primeru sta to »modra« in »rdeča« vrednost. Vrednost, ki nas zanima, označimo z vprašajem ali pa kar z neznanko x. Ta naj bo drugačne barve od podatkov. V našem primeru uporabimo zeleno barvo: Če pozorneje pogledamo desno stran lista, vidimo, da nam manjka le še korak do računa. Z zeleno smo obkrožili vrednost, ki nas zanima, torej »moder« in »rdeč« del skupaj. Besedo »skupaj« povezujemo z računsko operacijo »plus«, torej se bo račun glasil:
x=2+3∙2 Oziroma x=8. Maja in Jure sta torej kupila skupaj 8 tablic čokolade. Na koncu pa še napotek. Če je naloga preveč zahtevna zgolj za izpisovanje in obkrožanje podatkov, narišemo skico, kjer nastopajoče predmete in osebe narišemo v obliki čimbolj preprostih simbolov. Pri besedilnih nalogah imamo vedno podane neke podatke, "skrite" med besedilo, nakar sledi vprašanje (ali več vprašanj). Za marsikoga najtežji del reševanja take naloge predstavlja zapis računa, pogosto zaradi težav pri povezovanju abstraktnega s konkretnim oziroma, kot radi rečemo, "slabe predstave". Kaj pa, če bi nalogo "postavili na glavo"? Tako, da bi imeli najprej račun in bi si šele potem "izmislili" vprašanje? Vzemimo za primer naslednjo nalogo: Maja ima 3 jabolka, Jure pa 2. Razpolagamo torej z naslednjima dvema podatkoma:
Kaj lahko izračunamo? Kakšno bi bilo lahko vprašanje?
Poglejmo si nekaj primerov:
Ker si vprašanje zastavimo sami, imamo račun že "v glavi" in ga lažje povežemo s konkretnim problemom. S takimi vajami lahko enostavno in na bolj naraven način utrjujemo povezovanje abstraktnega "računskega" sveta s konkretnimi življenjskimi situacijami, saj je pot od računa do jabolk ali frnikol običajno lažja od poti v obratno smer. Za končni uspeh pa je seveda potrebno obvladati obe. Oglejmo si naslednji primer: Nika vsak dan preteče 5 kilometrov. Koliko kilometrov preteče v enem tednu? Za začetek obarvajmo besedilo s podatki z modro barvo, besedilo z vprašanji pa z rdečo: Nika vsak dan preteče 5 kilometrov. Koliko kilometrov preteče v enem tednu? V zvezku besedilo težko obarvate (razen če ga prepišete ;) ), lahko ga pa podčrtate. Nato označimo nepomembne podatke oziroma podatke, ki ne vplivajo na izračun:
Pomembne podatke pa označimo z rumenim markerjem: Podatki iz modrega dela so torej:
Na tem mestu se lahko malo ustavimo in razmišljamo:
Tudi v rdečem delu imamo podatek:
Zopet razmišljajmo:
Sedaj pa si oglejmo neznanko iz rdečega dela:
Končni razmislek:
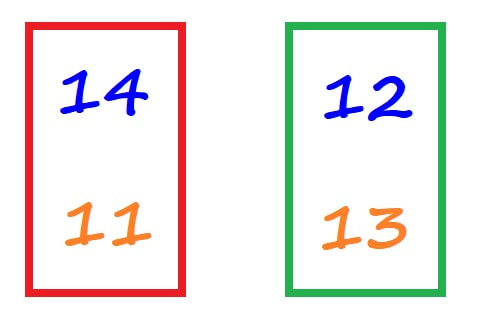
Končnega izračuna na tem mestu niti ne bom zapisal, saj namen zapisa ni rešiti besedilno nalogo, ampak omeniti možnost reševanja z vmesnim razmislekom. P.S. Dr'gač je pa rešitev 35, da se ne boste preveč tolk'l po glav' ;) Iz preprostega razloga - ker rezultat potem kar "pade pred nas" :) Oglejmo si naslednjo nalogo: V 2.a razredu je 14 deklic in 11 dečkov, v 2.b razredu pa 12 deklic in 13 dečkov. Koliko deklic je v obeh razredih skupaj? Kdor "obvlada", bo hitro ugotovil, da mora sešteti 14 in 12. Kaj pa tisti, ki se še učijo oziroma imajo težave pri razumevanju? Pomaga že, če z barvami "opremimo besedilo ... V 2.a razredu je 14 deklic in 11 dečkov, v 2.b razredu pa 12 deklic in 13 dečkov. Koliko deklic je v obeh razredih skupaj? ... še lažje pa nam bo, če situacijo skiciramo (poudarek je na "skiciramo", saj smo pri matematiki in ne pri LUM :) ) Sedaj, ko imamo sliko, bomo na vprašanja odgovorili veliko lažje. In to ne le na eno, tudi na kopico le-teh, recimo:
V oklepaju so barve, na katere moramo biti pri posameznem vprašanju pozorni. Led pri reševanju problemskih nalog učenci običajno prebijajo z osnovnimi nalogami "na plus in minus". Starši se ob reševanju domačih nalog velikokrat sprašujemo, kako bi jim pri tem pomagali. Tudi mi imamo za to nekaj predlogov :) Zadeve gredo običajno "lažje v glavo", če se jih učimo po več skupaj in med njimi iščemo neko relacijo, v našem primeru razliko. Kakšna je razlika med nalogami "na plus" in nalogami "na minus"? Podobna kot razlika med sodelovanjem in tekmovanjem. Zgornja dva primera lahko služita kot neka referenca, na katero se bodo učenci lahko vedno spomnili, kadar bodo "v škripcih".
Eno izmed osnovnih vodil pri učenju priporoča smer "od znanega k neznanemu", z drugimi besedami osvojitev obravnavanih lastnosti oziroma zakonitosti na dobro poznanem primeru in nato iskanje podobnih vzorcev še v drugih, manj "domačih" situacijah. "Na minus" pogosto računamo tudi pri nalogah, ko "z danes na jutri" nečesa zmanjka ali pa se nekaj poveča, nas pa zanima razlika, recimo takole: |
Arhiv
December 2023
kategorije
All
|







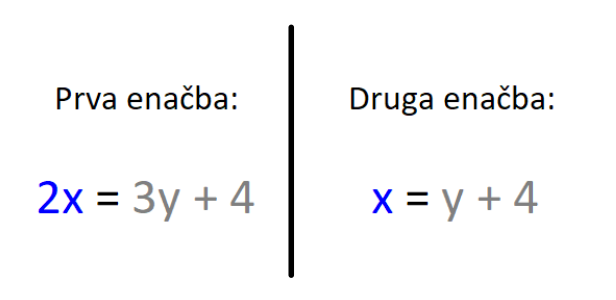
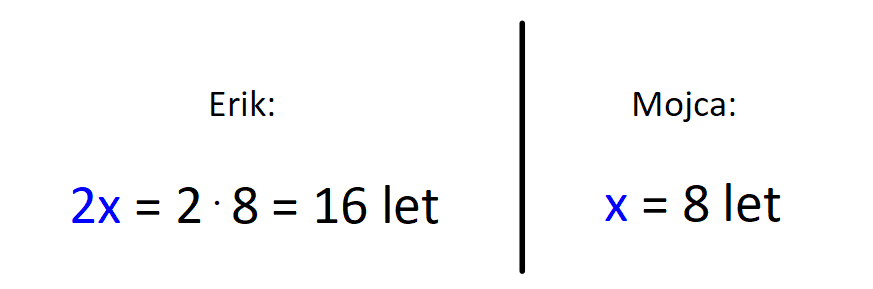





 RSS Feed
RSS Feed
