|
Napotki za reševanje take naloge:
Če naloga nima podanih številskih vrednosti, z upoštevanjem dejstva, da je sila vrvice na obeh straneh enaka, izenačite enačbi za obe uteži in izrazite željeno količino. Lahko si pomagate tudi z dejstvom, da je pospešek na obeh straneh škripca enak. Če je pri uteži na vodoravni podlagi F_vrvice enaka F_trenja, potem je rezultanta sil na obeh straneh in s tem tudi pospešek enaka nič. Bremeni mirujeta. Včasih lahko trenje pri uteži na vodoravni podlagi zanemarimo. V tem primeru za vodoravno utež velja: [F_vrvice = masa uteži na vodoravni podlagi * pospešek]
0 Comments
Na prvi pogled enostavna naloga, a se izkaže, da zna biti kar trd oreh ;)
Zato vam podamo nekaj napotkov:
Če naloga nima podanih številskih vrednosti, z upoštevanjem dejstva, da je sila vrvice na obeh straneh enaka, izenačite enačbi za obe uteži in izrazite željeno količino. Lahko si pomagate tudi z dejstvom, da je pospešek na obeh straneh škripca enak. Če sta bremeni slučajno enaki (z enako maso), potem je rezultanta sil na obeh straneh in s tem tudi pospešek enaka nič. Bremeni mirujeta. Če naloga nima podanih številskih vrednosti, je rezultat potrebno poiskati na podlagi sklepanja.
Pri sklepanju je zelo pomembno, da ugotovimo, v kakšnem razmerju sta veličini, ki ju primerjamo. To je lahko premo ali obratno. Za kakšno razmerje gre, najlažje ugotovimo s pomočjo enačbe. Ker med seboj lahko primerjamo le dve vrednosti hkrati, moramo morebitne ostale spremenljivke, ki nastopajo v enačbi, "zamrzniti". Kako to storiti, si oglejmo na primeru: Primer: Oče in sin imata enako površino stopal. Oče je težji (ima večjo maso) od sina. Pod čigavimi nogami je večji tlak? Rešitev:
Kdor se je pri fiziki učil sile, je verjetno naletel tudi na vzgon in famozni stavek "Vzgon je po velikosti enak teži izpodrinjene tekočine." Omenjeni stavek smo se naučili skoraj vsi, medtem ko ga je dejansko razumel manjši odstotek učencev. Vsaj na začetku. Če imate še vedno težave z razumevanjem, vam ponujamo še našo razlago. Začnimo z zgodbico. Smeško se odloči, da se bo malo potapljal. Ko je pod vodo, začuti, da ga nekaj vleče proti površju. Kaj neki bi bilo to?? No, potem Smeško prileze iz vode, se osuši in stopi na tehtnico. Sedaj pa nastopi naša domišljija (ki je seveda nujno potrebna za razumevanje vzgona). Zraven si predstavljajte Smeškovega "namišljenega prijatelja", ki je povsem enake velikosti kot Smeško, sestavljen pa je 100% iz vode: Iz enačb na zgornji sliki je razidno, da masa (m) Smeška določa velikost sile teže (usmerjena je navzdol proti središču Zemlje), masa njegovega "prijatelja" pa vzgon (usmerjen je naravnost navzgor oziroma ravno nasproti sili teže).
Poleg mas v enačbah na zgornji sliki nastopa tudi težni pospešek (g), ki je konstanta. V poenostavljeni obliki je njegova številska vrednost 10, tako da masam preprosto dodamo ničlo oz. premaknemo decimalno vejico v desno. Smeškota je torej k površju vlekla (oziroma natančneje, potiskala) sila, ki jo imenujemo vzgon. Le-ta je bila večja od njegove sile teže, kar pomeni, da je Smeško lažji od njegovega "prijatelja". Če bi Smeško in njegov dvojnik tehtala enako, bi Smeško lebdel, če pa bi bil pa Smeško težji, bi pa potonil na dno. Pretvorbe enot. Fizikalnih. Ampak ne tistega "simpl" premikanja decimalke levo in desno (pokukaj sem), temveč množenja in deljenja z vsemogočimi konstantami. Pa pojdimo kar lepo po vrsti:
Glede na zakon o ohranitvi energije je vsota energij (potencialna, kinetična, prožnostna, notranja, električna,...) vedno enaka, če ne posegata zraven toplota in delo.
Naloge najlažje rešujemo tako, da si izberemo posamične trenutke v času, kjer naredimo "popis" vrednosti energij. Primer1: V času t1 sankač miruje na klancu. Tedaj ima le potencialno energijo. Med časom t1 in t2 ga mi porinemo (vnesli smo delo in s tem povečali vrednost vsote energij) in ko v času t2 naredimo vnovičen "popis", ugotovimo da je vsota energij (potencialna in kinetična) za vrednost vloženega dela višja. Ko sankač v času t3 pridrvi skozi cilj, ima le še kinetično energijo, ki pa je enaka vsoti potencialne in kinetične energije v času t2 (delo in toplota vmes nista "mešala štren":) Primer2: V času t1 ima krogla le potencialno energijo. Tudi prožnostna energija v vzmeti pod njo je enaka 0, saj je vzmet v mirovnem položaju. V času t2 tik pred udarcem v vzmet ima krogla tako potencialno kot kinetično energijo, a nas stanje ne zanima, raje analiziramo čas t3, ko se celotna potencialna energija iz časa t1 pretvori v prožnostno. Tako je računanje lažje, saj se nam ni potrebno ukvarjati s kinetično energijo. Primer3: V času t1 ima sankač samo kinetično energijo. V času med t1 in t2 le-ta zapelje na pesek, ki ga nekoliko zaustavi. Sila trenja je opravila delo, ki se je v ozračje izločilo kot toplota. V času t2 ima sankač še vedno kinetično energijo, a zmanjšano za vrednost oddane toplote. Primer4: V času t1 imamo neko notranjo energijo. V vmesnem času med t1 in t2 pojemo čokolado, s katero pridobimo energijo. V času t2 je naša notranja energija manjša. V času med t2 in t3 stopimo na mraz in oddamo toploto. V času t3 je naša notranja energija spet manjša in sicer za oddano toploto. Med časom t3 in t4 se peljemo s kolesom in (pedalom) oddamo delo. V času t4 je naša notranja energija spet manjša...in tako naprej... Predstavljajmo si, da se ne moremo odtrgati od osebne tehtnice in jo s seboj vlačimo celo v dvigalo. Tega verjetno nihče od nas ne počne, ampak če bi, potem bi bili verjetno presenečeni, v nekaterih primerih prijetno, v drugih pa nekoliko manj prijetno. Poglejmo si, zakaj. Med
F = ma (oziroma "Fičo je mali avto") enaka nič, saj je pri mirovanju oz. enakomernem gibanju a=0, masa pa nikoli ne more biti enaka nič. Zanimivo postane, ko dvigalo
(F naše teže - F prožnostne sile vzmeti) = ma Določimo še pozitivno smer gibanja, ki jo bomo upoštevali v enačbi - ta naj bo navzdol. Tako velja:
Na kaj pri tej nalogi ne smemo pozabiti:
Alternativa: Tehtnico na vzmet lahko nadomestimo tudi s silomerom, pritrjenim na strop, na katerega je obešena utež. Ste vedeli, da za vse spodaj navedene primere lahko uporabite iste enačbe? Paziti je potrebno le na predznak pospeška, začetno hitrost ter v določenih primerih uporabiti težni pospešek, ki je konstanta. Enačbe se glasijo: Pri čemer Vo pomeni začetno hitrost, Vk končno hitrost, h pa pot (v x smeri) oz. višino (v y smeri).
Seveda. Le hitrost mora biti ves čas enaka. Torej imamo enakomerno gibanje.
Se boste pa verjetno vprašali "Zakaj pa je potrebno ob tem tako močno pritiskati pa plin?" Zato, ker moramo premagovati silo trenja (kolesa ob asfalt, ležaji pri vrtenju koles okoli osi) in silo (zračnega) upora. Ohmov zakon pravi:
Upornost je količnik med napetostjo na uporniku in tokom, ki teče skozi upornik. Enačbo si lahko zapomnimo s pomočjo naslednje slike: ...slika je še v pripravi, zato samo opis zanjo:
|


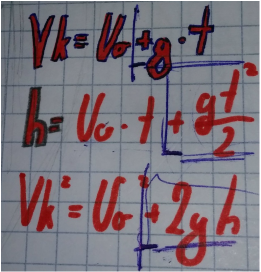
 RSS Feed
RSS Feed
