|
Enačbe lahko "premetavamo" na različne načine. Najbolj pravilen način je seveda izvedba enake računske operacije na obeh straneh enačbe, na primer: 2x = 6 | :2 x = 3 Obstajajo pa tudi razni triki in bližnjice, ki pa niso napačni, le nekoliko drugačna logika je "zadaj". In ravno to marsikomu pomaga pri razumevanju. Kdor ne mara ulomkov, ga bo verjetno razveselil naslednji način. Zamislimo si, da imamo enačbo: Če upoštevamo, da ulomek pomeni deljenje, lahko to enačbo zapišemo kot:
v = s : t Recimo, da v enačbo vnesemo podatke in dobimo: 120 = 60 : t Kot ste verjetno opazili, iščemo vrednost spremenljivke t. Pred njo je znak za deljenje, kar ni v redu, saj pomeni, da se nahaja v imenovalcu ulomka. Spraviti jo moramo "na vrh" (v števec ulomka) oziroma (če nastopa samostojno) pred njo postaviti znak za množenje. To dosežemo tako, da jo prestavimo na levi del enačbe: 120 ⋅ t = 60 Naloga je rešena, ko je iskana spremenljivka popolnoma sama na svoji strani enačbe. Do končnega izračuna nas torej loči le še vrednost 120. Ker se ta nahaja na skrajnem levem robu enačbe, predpostavimo, da je pred njo znak za množenje (120 je isto kot 1 ⋅ 120). Če jo prestavimo na desno stran enačbe, se znak za množenje spremeni v znak za deljenje in dobimo: t = 60 : 120 Znak za množenje pred t smo umaknili, saj se t nahaja na skrajnem levem robu enačbe. Lahko bi na levi strani enačbe zapisali tudi 1⋅ t, a nima smisla, saj množenje z 1 ničesar ne spremeni (1⋅ t = t). Na desni strani enačaja le še delimo in dobimo rezultat: t = 0,5 Pomni! Metoda temelji na dveh glavnih dejstvih:
Pozor! Sprememba operacije množenja z operacijo deljenja in obratno pri prehodu čez znak za enakost je možen samo v primerih, ko je na vsaki strani enačaja en sam člen! Če je členov več, omenjene metode ne moremo uporabiti! Dobro je vedeti: Če se iskana spremenljivka pojavi "na vrhu" (v števcu ulomka oziroma samostojno, ne v ulomku) na desni strani enačaja, enačbo preprosto obrnemo okoli (kar je na levi, damo na desno, kar je na desni pa na levo).
0 Comments
Ko naletimo na problem, se pogosto skušamo spomniti podobne situacije, ki smo jo pred časom uspešno rešili in uporabiti izkušnje, ki smo jih takrat pridobili. Če znamo množiti in deliti (ja, pri tem ne smemo pozabiti, da je tudi ulomek deljenje), si pri "premetavanju" nekaterih fizikalnih enačb lahko pomagamo na način, opisan na spodnji sliki: Ste ugotovili, za kaj gre? :)
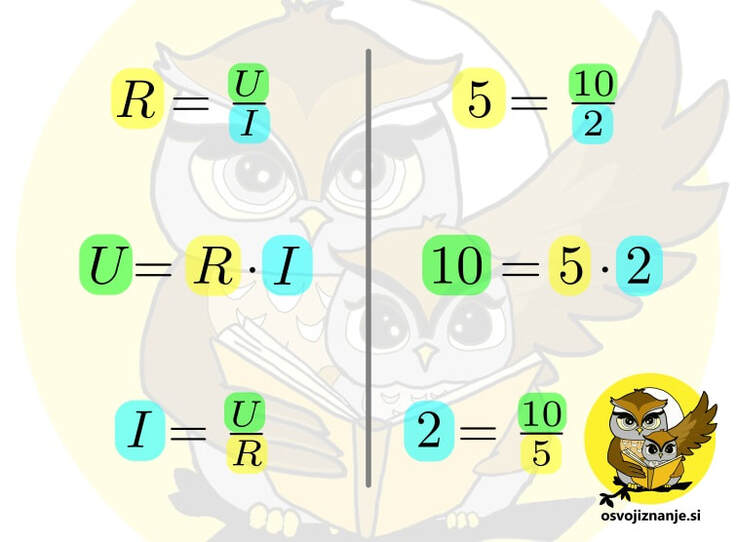
Na levi strani imamo enačbo za električno upornost v treh oblikah. Na desni strani pa tri preproste račune množenja in deljenja (ulomek pomeni deljenje, če slučajno iščete dvopičje :) ). Poglejmo prvo vrstico. Upornost (R) je napetost (U) deljeno s tokom (I). Ker imamo v enačbi deljenje, se poskusimo spomniti preprostega računa, ki vsebuje deljenje. Jaz sem izbral račun 10 deljeno z 2 je 5 (levo in desno stran sem zamenjal, da je izgled isti kot v enačbi). Enako ležeče spremenljivke (na levi) oziroma števila (na desni) so obarvane z enako barvo. V drugi vrstici (na levi) iščemo vrednost napetosti (U). Ta ustreza številu 10 (oba sta obarvana zeleno). Sedaj se vprašamo: "Kako iz preostalih dveh števil v enačbi dobim tretje?" V našem primeru sta to števili 2 in 5. 10 dobimo tako, da jih med seboj zmnožimo. Po logičnem sklepanju ugotovimo, da je tudi napetost (U) zmnožek upornosti (R) in toka (I). V tretji vrstici (na levi) iščemo vrednost toka (I). Ta ustreza številu 2 (oba sta obarvana modro). Zopet se vprašamo: "Kako iz preostalih dveh števil v enačbi dobim tretje?" V našem primeru sta to števili 10 in 5. 2 dobimo tako, da 10 delimo s 5. Po logičnem sklepanju ugotovimo, da je tudi tok (I) kvocient oz. količnik napetosti (U) in upornosti (R). Podobno si lahko pomagamo tudi pri enačbah, ki vsebujejo seštevanje in/ali odštevanje. Pri mešanih enačbah, ki vsebujejo tako množenje in/ali deljenje kot seštevanje in/ali odštevanje, pa je tak način reševanja že nekoliko bolj zakompliciran in ga ne priporočam. Pozor! Števila v enačbi naj bodo različna, da jih ločite med seboj. V našem primeru bi bila zelo slaba izbira števil 2, 2 in 4. Kot prvo, ne bi vedeli, katero dvojko imamo v mislih, dodatni problem pa bi bil še ta, da je 2+2 enako 2 krat 2 in bi imeli lahko problem tudi pri izbiri računskih operacij. |
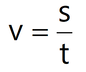
 RSS Feed
RSS Feed
