|
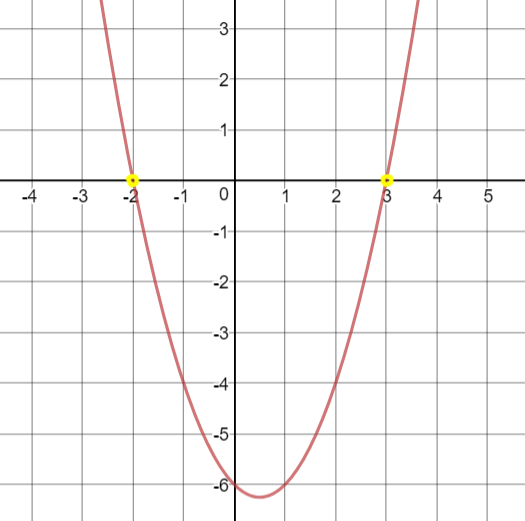
Na Twitter profilu matematika Matta Enlowa smo našli zanimivo objavo, ki povezuje znanje o izrazih, enačbah, ničlah funkcij in presečiščih grafa funkcije z abscisno (x) osjo. Za lažjo predstavo ga razložimo na primeru izraza v obliki polinoma (v našem primeru druge stopnje): p(x)=x²-x-6 Če polinom razstavimo, dobimo produkt linearnih faktorjev (v oklepajih, v našem primeru sta dva): p(x)=(x-3)(x+2) Če polinom izenačimo z 0, dobimo enačbo: (x-3)(x+2)=0 Rešitve te enačbe so hkrati ničle polinoma (v našem primeru sta dve): x₁=3 x₂=-2 O povezavi med produkti linearnih faktorjev in ničlah polinoma smo pisali že tule. Za polinom lahko rečemo, da je vrsta funkcije, ki jo dobimo s seštevanjem in množenjem. V razstavljeni obliki smo jo že zapisali: f(x)=(x-3)(x+2) Če funkcijo izenačimo z 0, dobimo ničle funkcije, ki so enake rešitvam enačbe: x₁=3 x₂=-2 Funkcijo lahko ponazorimo z njenim grafom: Točke, kjer graf seka abscisno (x) os koordinatnega sistema, imenujemo presečišča z x osjo. Vrednosti na x osi, kjer so presečišča, sovpadajo z rešitvami enačbe oziroma ničlami funkcije.
Omenjeno znanje z določenimi prilagoditvami in omejitvami lahko razširimo na vse izraze, ne le polinome.
0 Comments
Leave a Reply. |
 RSS Feed
RSS Feed
