Računi "na koliko" predstavljajo uvod v reševanje enačb, ki velja za eno temeljnih matematičnih veščin. Zato je zelo pomembno, da jih učenci dejansko razumejo in se jih ne učijo na pamet, kamoli uporabljajo različne "trike", kjer čez nekaj časa ne vemo več ali je plus ali minus, kaj se od česa odšteje itd. 

Pri teh računih nam lahko močno pomaga tudi vizualna predstava, predvsem pri pretvarjanju v "običajen" račun - tak, ki ima neznanko na svoji strani enačaja. S tem namenom je na spodnjih slikah vsakemu tipu računa dodan grafičen element v obliki dvojnega traka, pri katerem dolžina najdaljšega dela traka ustreza vsoti krajših delov. Med zgornjim in spodnjim delom velja torej enakost, tako kot v enačbi.

Seštevanje

Namig: Če ne vemo, katero število postaviti v najdaljši del traku, pomislimo, da je pri računu seštevanja na eni strani enačbe vedno vsota števil z druge strani enačaja in ker ta števila seštejemo med seboj, je vsota vedno največje število. V najdaljšem delu traku je torej število, ki v enačbi stoji na svoji strani enačbe. Logično, saj le-to zaseda celotno dolžino traku.

Odštevanje

Na hitro ponovimo, kaj lahko počnemo z matematičnimi izrazi.

Računske izraze (vsebujejo le številke, ki jim učeno rečemo koeficienti oziroma številski faktorji) izračunamo. Rešitev takega izraza je številka.

Algebrske izraze (poleg številk vsebujejo tudi črke oziroma spremenljivke) pa lahko:

• poenostavimo (na koncu dobimo "kačo" členov, med katerimi so plusi in minusi)
• razstavimo (na koncu dobimo le en člen, ki je običajno sestavljen iz zmnožka oklepajev)
• najprej poenostavimo in potem še razstavimo.

Če pa spremenljivkam dodelimo številske vrednosti, algebrski izraz postane računski in ga lahko izračunamo.

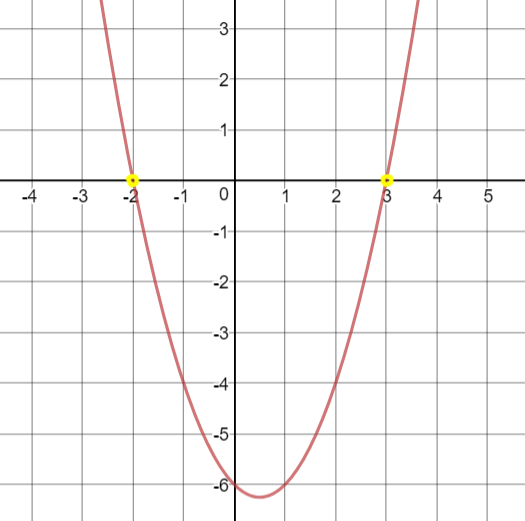
Na Twitter profilu matematika Matta Enlowa smo našli zanimivo objavo, ki povezuje znanje o izrazih,  enačbah, ničlah funkcij in presečiščih grafa funkcije z abscisno (x) osjo.

Za lažjo predstavo ga razložimo na primeru izraza v obliki polinoma (v našem primeru druge stopnje):

p(x)=x²-x-6

Če polinom razstavimo, dobimo produkt linearnih faktorjev (v oklepajih, v našem primeru sta dva):

p(x)=(x-3)(x+2)

Če polinom izenačimo z 0, dobimo enačbo:

(x-3)(x+2)=0

Rešitve te enačbe so hkrati ničle polinoma (v našem primeru sta dve):

x₁=3
x₂=-2

O povezavi med produkti linearnih faktorjev in ničlah polinoma smo pisali že tule.

Za polinom lahko rečemo, da je vrsta funkcije, ki jo dobimo s seštevanjem in množenjem. V razstavljeni obliki smo jo že zapisali:

f(x)=(x-3)(x+2)

​Če funkcijo izenačimo z 0, dobimo ničle funkcije, ki so enake rešitvam enačbe:

x₁=3
x₂=-2

Funkcijo lahko ponazorimo z njenim grafom: